题目内容
已知等差数列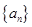 的公差
的公差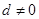 ,它的前
,它的前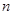 项和为
项和为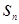 ,若
,若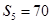 ,且
,且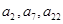 成等比数列.(1) 求数列
成等比数列.(1) 求数列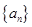 的通项公式;(2)设数列
的通项公式;(2)设数列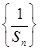 的前
的前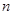 项和为
项和为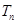 ,求证:
,求证: .
.
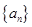 的公差
的公差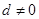 ,它的前
,它的前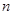 项和为
项和为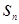 ,若
,若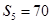 ,且
,且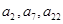 成等比数列.(1) 求数列
成等比数列.(1) 求数列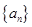 的通项公式;(2)设数列
的通项公式;(2)设数列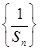 的前
的前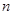 项和为
项和为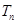 ,求证:
,求证: .
.(1)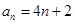 ;(2)
;(2) .
.
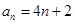 ;(2)
;(2) .
.试题分析:(1)求通项公式的关键是求出
 ,所以通过等差数列的求和公式和等比中项将两个已知条件都转化为
,所以通过等差数列的求和公式和等比中项将两个已知条件都转化为 的关系式,解出
的关系式,解出 ,就可以求出等差数列的通项公式了.(2)先用裂项相消法求出
,就可以求出等差数列的通项公式了.(2)先用裂项相消法求出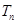 的值,再通过作差法看出数列
的值,再通过作差法看出数列 是递增数列,求出最大值和最小值,即得到证明.
是递增数列,求出最大值和最小值,即得到证明.试题解析:(1)
 数列
数列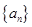 是等差数列且
是等差数列且 ,
,
 . ① 2分
. ① 2分 
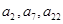 成等比数列,
成等比数列,
 即
即 ② 4分
② 4分 由①,②解得
 或
或 (舍去) 5分
(舍去) 5分
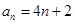 6分
6分(2)证明;由(1)可得
 , 7分
, 7分所以
 . 8分
. 8分所以


 . 10分
. 10分 ∵
 ,∴
,∴  . 11分
. 11分∵
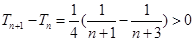 ,∴数列
,∴数列 是递增数列,∴
是递增数列,∴  . 13分
. 13分∴
 . 14分
. 14分
练习册系列答案
相关题目
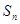 为其前n项和
为其前n项和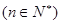 ,且
,且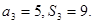
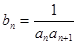 ,求数列
,求数列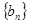 的前
的前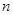 项和
项和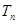 .
.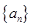 中,
中,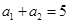 ,
,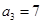 ,记数列
,记数列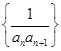 的前
的前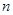 项和为
项和为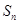 .
.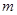 、
、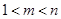 ,使得
,使得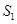 、
、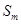 、
、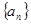 的前
的前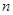 项和为
项和为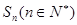 ,若
,若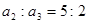 ,则
,则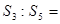 _________.
_________.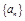 中的
中的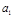 、
、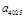 是函数
是函数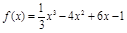 的极值点,则
的极值点,则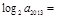 ( )
( )
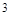

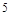
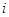 行第
行第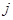 列的数为
列的数为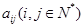 ,则
,则
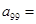 ;
;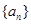 中,
中,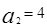 ,其前n项和
,其前n项和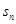 满足
满足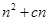
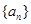 是等差数列,期中
是等差数列,期中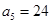 ,
,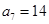
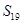
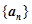 中,2a4+a7=3,则数列
中,2a4+a7=3,则数列