题目内容
用数学归纳法证明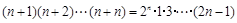 ,从
,从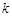 到
到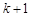 ,左边需要增乘的代数式为()
,左边需要增乘的代数式为()
A.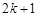 | B.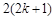 | C.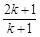 | D.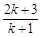 |
B
解析试题分析:当n=k时,左边等于(k+1)(k+2)…(k+k)=(k+1)(k+2)…(2k),当n=k+1时,左边等于(k+2)(k+3)…(k+k)(2k+1)(2k+2),故从“k”到“k+1”的证明,左边需增添的代数式是  =2(2k+1),故答案为B.
=2(2k+1),故答案为B.
考点:数学归纳法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列推理中属于归纳推理且结论正确的是( )
| A.设数列﹛an﹜的前n项和为sn,由an=2n﹣1,求出s1 =12 , s2=22,s3=32,…推断sn=n2 |
B.由 cosx,满足 cosx,满足 对 对 x∈R都成立,推断 x∈R都成立,推断 为奇函数。 为奇函数。 |
C.由圆 的面积 的面积 推断:椭圆 推断:椭圆 (a>b>0)的面积s=πab (a>b>0)的面积s=πab |
| D.由(1+1)2>21,(2+1)2>22,(3+1)2 >23,…,推断对一切正整数n,(n+1)2>2n |
下面几种推理中是演绎推理的序号为( )
A.半径为 圆的面积 圆的面积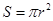 ,则单位圆的面积 ,则单位圆的面积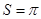 ; ; |
| B.由金、银、铜、铁可导电,猜想:金属都可导电; |
| C.由平面三角形的性质,推测空间四面体性质; |
D.由平面直角坐标系中圆的方程为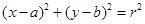 ,推测空间直角坐标系中球的方程为 ,推测空间直角坐标系中球的方程为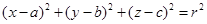 . . |
已知数列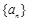 的前
的前 项和为
项和为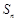 ,且
,且 ,
,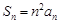
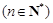 ,可归纳猜想出
,可归纳猜想出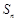 的表达式为( )
的表达式为( )
A. | B. | C.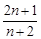 | D.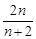 |
平面内有n条直线,最多可将平面分成f(n)个区域,则f(n)的表达式为( )
| A.n+1 | B.2n |
C.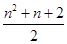 | D.n2+n+1 |
圆周上2个点可连成1条弦,这条弦可将圆面划分成2部分;圆周上3个点可连成3条弦,这3条弦可将圆面划分成4部分;圆周上4个点可连成6条弦,这6条弦最多可将圆面划分成8部分.则这些弦最多可把圆面分成 ( ) 部分
| A.2n-1 | B.2n | C.2n+1 | D.2n+2 |
观察下列事实|x|+|y|=1的不同整数解(x,y)的个数为4,|x|+|y|=2的不同整数解(x,y)的个数为8,|x|+|y|=3的不同整数解(x,y)的个数为12 ….则|x|+|y|=20的不同整数解(x,y)的个数为( )
| A.76 | B.80 | C.86 | D.92 |
观察下列各式:72=49,73=343,74=2401,…,则72011的末两位数字为( )
| A.01 | B.43 | C.07 | D.49 |
