题目内容
 如图:PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成角是30°,点F是PB的中点,E为边BC上的动点.
如图:PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成角是30°,点F是PB的中点,E为边BC上的动点.(1)证明:无论点E在边BC的何处,都有PE⊥AF
(2)当BE等于何值时,二面角P-DE-A的大小为45°
(3)在(2)问的条件下,求P点到角AEF的距离.
分析:(1)由题设条件及图形可得出AF⊥平面PBE,由线面垂直的定义可得出无论点E在边BC的何处两线都垂直.
(2)以A为坐标原点,AD,AB,AP为x轴,y轴,z轴,建立如图所示的空间直角坐标系,由题设知PD=2,AB=
,则P(0,0,1),D(
,0,0),设A(a,1,0),(0≤a≤
),故
=(a,1,-1),
=(
,0,-1),由向量法知BE=
-
时,二面角P-DE-A的大小为45°.
(3)当BE=
-
时,A(0,0,0),E(
-
,1,0),F(0,
,
),故
=(
-
,1,0),
=(0,
,
),由向量法能求出P点到面AEF的距离.
(2)以A为坐标原点,AD,AB,AP为x轴,y轴,z轴,建立如图所示的空间直角坐标系,由题设知PD=2,AB=
| 3 |
| 3 |
| 3 |
| PE |
| PD |
| 3 |
| 3 |
| 2 |
(3)当BE=
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| AE |
| 3 |
| 2 |
| AF |
| 1 |
| 2 |
| 1 |
| 2 |
解答: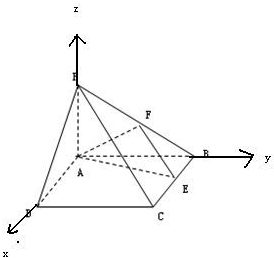 (1)证明:∵PA⊥平面ABCD,BE?平面ABCD,
(1)证明:∵PA⊥平面ABCD,BE?平面ABCD,
∴EB⊥PA.又EB⊥AB,AB∩AP=A,AB,AP?平面PAB,
∴EB⊥平面PAB,
又AF?平面PAB,
∴AF⊥BE.
又PA=AB=1,点F是PB的中点,
∴AF⊥PB,又∵PB∩BE=B,PB,BE?平面PBE,
∴AF⊥平面PBE.
∵PE?平面PBE,∴AF⊥PE.
即不论点E在边BC上何处,都有PE⊥AF成立.
(2)解:以A为坐标原点,AD,AB,AP为x轴,y轴,z轴,建立如图所示的空间直角坐标系,
∵PA⊥平面ABCD,ABCD是矩形,PA=AB=1,
PD与平面ABCD所成角是30°,点F是PB的中点,E为边BC上的动点,
∴PD=2,AB=
,则P(0,0,1),D(
,0,0),设A(a,1,0),(0≤a≤
),
∴
=(a,1,-1),
=(
,0,-1),
设平南PDE的法向量
=(x1,y1,z1),
则
,
∴
=(1,
-a,
),
面ADE的法向量是
=(0,0,1),
∵二面角P-DE-A的大小为45°
∴|cos<
,
>|=|
|=
,
解得a=
-
,或a=
+
(舍去).
∴BE=
-
时,二面角P-DE-A的大小为45°.
(3)当BE=
-
时,
A(0,0,0),E(
-
,1,0),F(0,
,
),
∴
=(
-
,1,0),
=(0,
,
),
设面AEF的法向量
=(x2,y2,z2),
则
,
∴
=(1,
-
,
-
),
∵
=(0,0,1),
∴P点到面AEF的距离d=
=
=
=
.
 (1)证明:∵PA⊥平面ABCD,BE?平面ABCD,
(1)证明:∵PA⊥平面ABCD,BE?平面ABCD,∴EB⊥PA.又EB⊥AB,AB∩AP=A,AB,AP?平面PAB,
∴EB⊥平面PAB,
又AF?平面PAB,
∴AF⊥BE.
又PA=AB=1,点F是PB的中点,
∴AF⊥PB,又∵PB∩BE=B,PB,BE?平面PBE,
∴AF⊥平面PBE.
∵PE?平面PBE,∴AF⊥PE.
即不论点E在边BC上何处,都有PE⊥AF成立.
(2)解:以A为坐标原点,AD,AB,AP为x轴,y轴,z轴,建立如图所示的空间直角坐标系,
∵PA⊥平面ABCD,ABCD是矩形,PA=AB=1,
PD与平面ABCD所成角是30°,点F是PB的中点,E为边BC上的动点,
∴PD=2,AB=
| 3 |
| 3 |
| 3 |
∴
| PE |
| PD |
| 3 |
设平南PDE的法向量
| n1 |
则
|
∴
| n1 |
| 3 |
| 3 |
面ADE的法向量是
| n |
∵二面角P-DE-A的大小为45°
∴|cos<
| n |
| n1 |
| ||||
|
| ||
| 2 |
解得a=
| 3 |
| 2 |
| 3 |
| 2 |
∴BE=
| 3 |
| 2 |
(3)当BE=
| 3 |
| 2 |
A(0,0,0),E(
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| AE |
| 3 |
| 2 |
| AF |
| 1 |
| 2 |
| 1 |
| 2 |
设面AEF的法向量
| n2 |
则
|
∴
| n2 |
| 2 |
| 3 |
| 3 |
| 2 |
∵
| AP |
∴P点到面AEF的距离d=
|
| ||||
|
|
| ||||
|
| ||||
2
|
| ||
| 5 |
点评:本题考查无论点E在边BC的何处,都有PE⊥AF的证明,求当BE等于何值时,二面角P-DE-A的大小为45°,求P点到角AEF的距离.考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易出错.是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,M,N分别是AB,PC的中点.
如图,PA⊥平面ABCD,四边形ABCD是正方形,PA=AD=2,M,N分别是AB,PC的中点. 如图,PA⊥平面AC,四边形ABCD是矩形,E、F分别是AB、PD的中点.
如图,PA⊥平面AC,四边形ABCD是矩形,E、F分别是AB、PD的中点. 如图,PA⊥平面ABC,AC⊥BC,AB=2,
如图,PA⊥平面ABC,AC⊥BC,AB=2, (2010•天津模拟)如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点
(2010•天津模拟)如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点 如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点F是PB的中点,点E在边BC上移动.
如图,PA⊥平面ABCD,四边形ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点F是PB的中点,点E在边BC上移动.