题目内容
(本题满分16分)
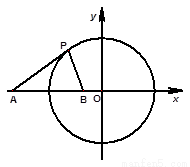
已知圆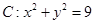 ,点
,点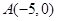 ,直线
,直线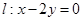 .
.
⑴求与圆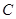 相切,且与直线
相切,且与直线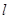 垂直的直线方程;
垂直的直线方程;
⑵在直线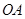 上(
上(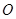 为坐标原点),存在定点
为坐标原点),存在定点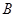 (不同于点
(不同于点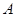 ),满足:对于圆
),满足:对于圆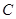 上任一点
上任一点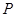 ,都有
,都有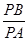 为一常数,试求所有满足条件的点
为一常数,试求所有满足条件的点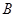 的坐标.
的坐标.
【答案】
(1)直线方程为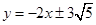
(2)存在点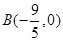 对于圆
对于圆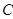 上任一点
上任一点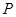 ,都有
,都有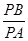 为常数
为常数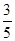 。
。
【解析】解:⑴设所求直线方程为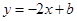 ,即
,即 ,
,
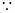 直线与圆相切,∴
直线与圆相切,∴ ,得
,得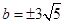 ,
,
∴所求直线方程为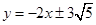 -----------5分
-----------5分
⑵方法1:假设存在这样的点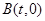 ,
,
当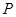 为圆
为圆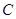 与
与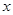 轴左交点
轴左交点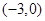 时,
时,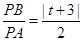 ;
;
当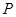 为圆
为圆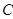 与
与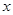 轴右交点
轴右交点 时,
时,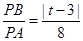 ,
,
依题意,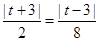 ,解得,
,解得,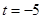 (舍去),或
(舍去),或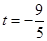 。 -----------------8分
。 -----------------8分
下面证明 点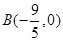 对于圆
对于圆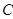 上任一点
上任一点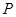 ,都有
,都有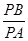 为一常数。
为一常数。
设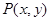 ,则
,则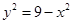 ,
,
∴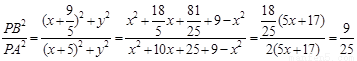 ,
,
从而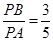 为常数。
-------------15分
为常数。
-------------15分
方法2:假设存在这样的点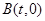 ,使得
,使得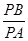 为常数
为常数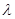 ,则
,则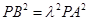 ,
,
∴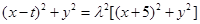 ,将
,将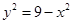 代入得,
代入得,
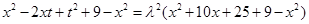 ,即
,即
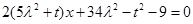 对
对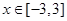 恒成立, ----------------8分
恒成立, ----------------8分
∴ ,解得
,解得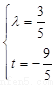 或
或 (舍去),
(舍去),
所以存在点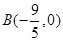 对于圆
对于圆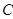 上任一点
上任一点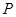 ,都有
,都有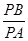 为常数
为常数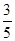 。 ------------15分
。 ------------15分

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目


 在
在 上的单调性;
上的单调性; ,使
,使 ,则称
,则称 的不动点,现已知该函数有且仅有一个不动点,求
的不动点,现已知该函数有且仅有一个不动点,求 的值;
的值; 在
在