题目内容

12．已知a=log62，b=log63，则a3+b3+3ab=1．

分析 由已知可得a+b=1，进而由a3+b3+3ab=（a+b）3-3ab（a+b）+3ab，代入可得答案．

解答 解：∵a=log62，b=log63，
∴a+b=1，
∴a3+b3+3ab=（a+b）3-3ab（a+b）+3ab=1-3ab+3ab=1，
故答案为：1．

点评 本题考查的知识点是对数的运算性质，其中根据已知得到a+b=1，是解答的关键．

练习册系列答案
相关题目
2．已知向量$\overrightarrow{a}$=（sin$\frac{x}{3}$，-1），$\overrightarrow{b}$=（$\sqrt{3}$，cos$\frac{x}{3}$），且函数f（x）满足f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$．
（1）求函数f（x）的解析式；
（2）求f（$\frac{5}{4}$π）的值；
（3）设α，β∈[0，$\frac{π}{2}$]，f（3α+$\frac{π}{2}$）=$\frac{10}{13}$，f（3β+2π）=$\frac{6}{5}$，求cos（α+β）的值．
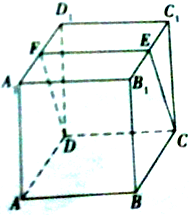3．如图，在正方体ABCD-A1B1C1D1中，E、F分别是棱B1C1，A1D1的中点，求证：平面ABB1A1与平面CDFE相交．
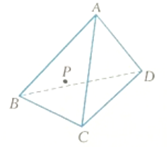20．如图，一个四面体木块ABCD，在△ABC的面内有一点P，要经过点P在平面ABC内画一条直线l，使l⊥AD，怎样画？写出作法，并给予证明．
7．已知过点P（O，1）斜率为k的直线l交双曲线x2-$\frac{{y}^{2}}{3}$=1于A，B两点．
（1）求k的取值范围；
（2）当k=1时，求△AOB的面积．
17．填空：已知ABCD为一个平行四边形，对角线AC与BD相交于点O，则
$\overrightarrow{AB}$+$\overrightarrow{AD}$=$\overrightarrow{AC}$；$\overrightarrow{AB}$-$\overrightarrow{AD}$=$\overrightarrow{DB}$；
$\overrightarrow{BA}$-$\overrightarrow{BC}$=$\overrightarrow{CA}$；$\overrightarrow{BC}$-$\overrightarrow{BA}$=$\overrightarrow{AC}$；
$\overrightarrow{OA}$-$\overrightarrow{OB}$=$\overrightarrow{BA}$；$\overrightarrow{OD}$-$\overrightarrow{OA}$=$\overrightarrow{AD}$．
4．函数y=$\frac{1}{2}$sinπx的递增区间是[2k-$\frac{1}{2}$，2k+$\frac{1}{2}$]，k∈Z．
1．已知函数f（x）=$\left\{\begin{array}{l}{-1-x，（-1＜x＜0）}\\{x，（0≤x≤1）}\end{array}\right.$，则f-1（$\frac{1}{3}$）=$\frac{1}{3}$．
2．已知a，b，c，d∈R且ab＞0，$-\frac{c}{a}$$＞-\frac{d}{b}$（　　）
A．bc＜adB．bc＞adC．$\frac{a}{c}$$＜\frac{1}{b}$D．$\frac{a}{c}$$＜\frac{b}{d}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网