题目内容
3.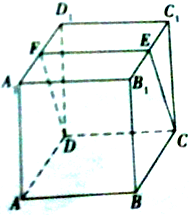 如图,在正方体ABCD-A1B1C1D1中,E、F分别是棱B1C1,A1D1的中点,求证:平面ABB1A1与平面CDFE相交.
如图,在正方体ABCD-A1B1C1D1中,E、F分别是棱B1C1,A1D1的中点,求证:平面ABB1A1与平面CDFE相交.
分析 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,分别求出平面DCEF的法向量和平面ABB1A1的法向量,利用向量法能证明平面ABB1A1与平面CDFE相交.
解答 证明:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
设正方体ABCD-A1B1C1D1的棱长为2,
则D(0,0,0),C(0,2,0),F(1,0,2),
$\overrightarrow{DC}$=(0,2,0),$\overrightarrow{DF}$=(1,0,2),
设平面DCEF的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DC}=2y=0}\\{\overrightarrow{n}•\overrightarrow{DF}=x+2z=0}\end{array}\right.$,取z=1,得$\overrightarrow{n}$=(-2,0,1),
又平面ABB1A1的法向量$\overrightarrow{m}$=(1,0,0),
cos<$\overrightarrow{m},\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}|•|\overrightarrow{n}|}$=$\frac{-2}{\sqrt{3}}$=-$\frac{2\sqrt{3}}{3}$,
∴平面ABB1A1与平面CDFE相交.
点评 本题考查两平面相交的证明,是基础题,解题时要注意向量法的合理运用.

练习册系列答案
相关题目
13.在△ABC中,若(b-bcosB)sinA=a(sinB-sinCcosC),则这个三角形是( )
| A. | 等腰直角三角形 | B. | 底角不等于45°的等腰三角形 | ||
| C. | 等腰三角形或直角三角形 | D. | 锐角不等于45°的直角三角形 |
14.已知直线l的参数方程为$\left\{\begin{array}{l}{x=t}\\{y=t}\end{array}\right.$ (t为参数),圆C的极坐标方程为ρ=2cos θ,则圆C的圆心到直线l的距离为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{\sqrt{2}}{4}$ |