题目内容
已知m、n是两条不重合的直线,α、β、γ是三个两两不重合的平面,给出下列四个命题:
①若m⊥α,m⊥β,则α∥β;
②若α⊥γ,β⊥α,则α∥β;
③若m∥α,n∥β,m∥n,则α∥β;
④若m、n是异面直线,m⊥α,m∥β,n⊥β,n∥α,则α⊥β
其中真命题是( )
| A.①和② | B.①和③ | C.③和④ | D.①和④ |
D
解析试题分析:垂直于同一直线的两个平面平行,所以“①若m⊥α,m⊥β,则α∥β”正确;
结合“墙角结构”可知“②若α⊥γ,β⊥α,则α∥β”不正确;
由平面平行的判定定理知“③若m∥α,n∥β,m∥n,则α∥β”不正确;至此可以选D。
考点:本题主要考查立体几何中线面平行、垂直关系。
点评:容易题,结合命题条件,对照定理、公理加以判断。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知一个棱长为 的正方体的顶点都在球面上,则球的表面积等于( )
的正方体的顶点都在球面上,则球的表面积等于( )
A. | B. |
C. | D. |
下列说法正确的是( )
| A.有两个面平行,其余各面都是四边形的几何体叫棱柱. |
| B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱. |
| C.有一个面是多边形,其余各面都是三角形的几何体叫棱锥. |
| D.棱台各侧棱的延长线交于一点. |
若某几何体的三视图如图1所示,则此几何体的表面积是( )
A. | B. | C. | D. |
如图,E、F分别是正方形 的边
的边 的中点,沿SE、SF、EF将它折成一个几何体,使
的中点,沿SE、SF、EF将它折成一个几何体,使 重合,记作D,给出下列位置关系:①SD
重合,记作D,给出下列位置关系:①SD 面EFD ; ②SE
面EFD ; ②SE 面EFD;③DF
面EFD;③DF SE;④EF
SE;④EF 面SE其中成立的有( )
面SE其中成立的有( )
| A.①与② | B.①与③ |
| C.②与③ | D.③与④ |

 ,BC=1,E为线段DC上一动点,现将
,BC=1,E为线段DC上一动点,现将 AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为
AED沿AE折起,使点D在面ABC上的射影K在直线AE上,当E从D运动到C,则K所形成轨迹的长度为

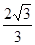


 是正三角形,AD
是正三角形,AD 平面ABC,AD=2AB=6,则该球的体积为 ( )
平面ABC,AD=2AB=6,则该球的体积为 ( ) B.
B. C.
C. D.
D.