题目内容
点A、B、C、D均在同一球面上，其中
是正三角形，AD
平面ABC,AD=2AB=6,则该球的体积为 ( )
A.
B.
C.
D.
A
解析试题分析：由题意画出几何体的图形如图，
把A、B、C、D扩展为三棱柱，
上下底面中心连线的中点与A的距离为球的半径，
AD=2AB=6，OE=3，△ABC是正三角形，
所以AE=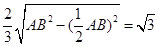
．
AO=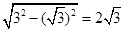
．
所求球的体积为
故选A．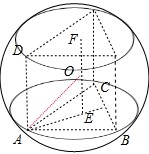
考点：本题主要考查球的体积和表面积；棱锥的结构特征；球内接多面体。
点评：利用割补法结合球内接多面体的几何特征求出球的半径是解题的关键．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
下列几何体各自的三视图中,有且仅有两个视图相同的是( )
①正方体 ②圆锥 ③正三棱台 ④正四棱锥
| A．①② | B．①③ | C．①③ | D．②④ |
。则该几何体的俯视图可以是（ ）
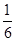
的等腰三角形,侧视图是半径为1的半圆，则该几何体的体积是（ ）
