题目内容
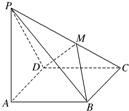
如图,四棱锥P-ABCD的底面ABCD是菱形,∠BCD=60°,PA⊥面ABCD,E是AB的中点,F是PC的中点.
(Ⅰ)求证:面PDE⊥面PAB;
(Ⅱ)求证:BF∥面PDE.
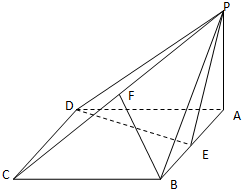
(Ⅰ)求证:面PDE⊥面PAB;
(Ⅱ)求证:BF∥面PDE.

证明:(Ⅰ)∵底面ABCD是菱形,∠BCD=60°
∴△ABD为正三角形E是AB的中点,DE⊥AB-----------------------------------(2分)
∵PA⊥面ABCD,DE?面ABCD
∴DE⊥AP-----------------------------------(4分)
∵AB∩AP=A
∴DE⊥面PAB
∵DE?面PDE
∴面PDE⊥面PAB-----------------------------------(6分)
(Ⅱ)取PD的中点G,连结FG,GE,-----------------------------------(8分)
∵F,G是中点,∴FG∥CD且FG=
CD
∴FG与BE平行且相等,
∴BF∥GE-----------------------------------(10分)
∵GE?面PDE
∴BF∥面PDE.-----------------------------------(12分)

∴△ABD为正三角形E是AB的中点,DE⊥AB-----------------------------------(2分)
∵PA⊥面ABCD,DE?面ABCD
∴DE⊥AP-----------------------------------(4分)
∵AB∩AP=A
∴DE⊥面PAB
∵DE?面PDE
∴面PDE⊥面PAB-----------------------------------(6分)
(Ⅱ)取PD的中点G,连结FG,GE,-----------------------------------(8分)
∵F,G是中点,∴FG∥CD且FG=
| 1 |
| 2 |
∴FG与BE平行且相等,
∴BF∥GE-----------------------------------(10分)
∵GE?面PDE
∴BF∥面PDE.-----------------------------------(12分)


练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
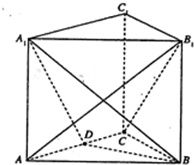
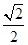 ,这样的点P的个数是( )
,这样的点P的个数是( )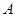 在平面
在平面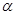 内,其余顶点在
内,其余顶点在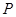 是正方体的其余四个顶点中的一个,则
是正方体的其余四个顶点中的一个,则