题目内容
已知函数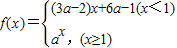
在（-∞，+∞）上单调递减，那么实数a的取值范围是 ．
【答案】分析：由已知中函数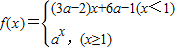
在（-∞，+∞）上单调递减，则在两个分段上函数均为减函数，且当x=1时，按照x＜1得到的函数值不小于按照x≥1得到的函数值．由此关于a的不等式，解不等式即可得到答案．
解答：解：∵数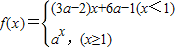
在（-∞，+∞）上单调递减，
∴
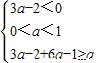
解得：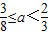
故答案为：[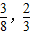
）
点评：本题考查的知识点是函数的单调性的性质，其中根据分段函数单调性的确定方法，构造出满足条件的关于a的不等式，是解答本题的关键．
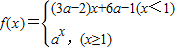在（-∞，+∞）上单调递减，则在两个分段上函数均为减函数，且当x=1时，按照x＜1得到的函数值不小于按照x≥1得到的函数值．由此关于a的不等式，解不等式即可得到答案．解答：解：∵数
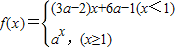在（-∞，+∞）上单调递减，∴
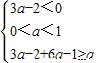
解得：
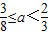
故答案为：[
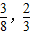）点评：本题考查的知识点是函数的单调性的性质，其中根据分段函数单调性的确定方法，构造出满足条件的关于a的不等式，是解答本题的关键．
练习册系列答案
相关题目