题目内容
如图，一条电路从A处到B处接通时，可有 条不同的线路．
考点：计数原理的应用
专题：应用题,排列组合
分析：本题是一个分类计数问题，按上、中、下三条线路可分为三类，上线路中有3种，中线路中有一种，下线路中有2×2种．根据分类计数原理得到结果．
解答：
解：由题意知本题是一个分类计数问题，
∵按上、中、下三条线路可分为三类，
上线路中有3种，
中线路中有一种，
下线路中有2×2=4（种）．
根据分类计数原理，共有3+1+4=8（种）．
故答案为：8．
∵按上、中、下三条线路可分为三类，
上线路中有3种，
中线路中有一种，
下线路中有2×2=4（种）．
根据分类计数原理，共有3+1+4=8（种）．
故答案为：8．
点评：本题考查分类计数原理，对于分类问题一定要看清楚做完这件事需要分成几类方法，每类方法各有几种方法，把所有的结果数相加即可．
练习册系列答案
相关题目
设f（x）=xlnx，若f′（x0）=2，则x0等于（ ）
| A、e2 | ||
| B、e | ||
C、
| ||
| D、ln2 |
已知数列{an}满足：a1=-
，an+1=1-
，则a2009=（ ）
| 1 |
| 4 |
| 1 |
| an |
A、
| ||
| B、5 | ||
C、-
| ||
D、
|
若数列{an}的通项公式为an=
，其前n项和为
，则n为（ ）
| 1 |
| (n+1)(n+2) |
| 7 |
| 18 |
| A、5 | B、6 | C、7 | D、8 |
在平面直角坐标系中，不等式组
，（a是常数）表示的平面区域面积是9，那么实数a的值为（ ）
|
A、3
| ||
B、-3
| ||
| C、-5 | ||
| D、1 |
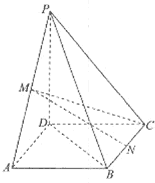如图，在四棱锥P-ABCD中，底面ABCD是正方形，PD⊥底面ABCD，M、N分别为PA、BC的中点，且PD=AD=1，