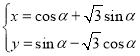题目内容
【题目】已知函数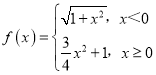 ,点
,点![]() 是函数
是函数![]() 图象上不同的两点,则
图象上不同的两点,则![]() 为坐标原点)的取值范围是( )
为坐标原点)的取值范围是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】A
【解析】
根据分段函数的表达式,分别求出对应切线和双曲线渐近线的倾斜角,结合位置关系判断∠AOB的大小即可.
当x<0时,y=![]() ,则y2=1+x2,当
,则y2=1+x2,当![]() 时,
时,![]() ,作出函数图象:
,作出函数图象:
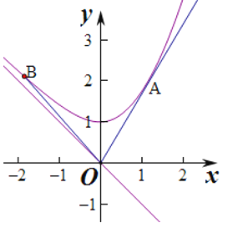
当x<0时,y=![]() ,则y2=1+x2,
,则y2=1+x2,
即![]() ,为双曲线在第二象限的一部分,
,为双曲线在第二象限的一部分,
双曲线的渐近线方程为![]() ,
,
若B在双曲线上,则∠BOy的范围是0<∠BOy<![]() ,
,
设当x≥0时,过原点的切线与f(x)=![]() x2+1,相切,
x2+1,相切,
设切点为![]() ,
,
则f′(x)=![]() x,即切线斜率k=
x,即切线斜率k=![]() a,
a,
则切线方程为![]() ,
,
∵切线过原点,
∴![]() ,
,
即![]() ,
,
得![]()
![]() =1,即
=1,即![]() =
=![]() ,则
,则![]() =
=![]() ,
,
则切线斜率![]() ,即切线倾斜角为
,即切线倾斜角为![]() ,
,
则∠AOy的最大值为![]() ,
,
即0≤∠AOy≤![]() ,
,
则0<∠AOy+∠BOy<![]() ,
,
即0<∠AOB<![]() ,
,
故选:A.

【题目】下表是某电器销售公司2018年度各类电器营业收入占比和净利润占比统计表:
空调类 | 冰箱类 | 小家电类 | 其它类 | |
营业收入占比 |
|
|
|
|
净利润占比 |
|
|
|
|
则下列判断中不正确的是( )
A. 该公司2018年度冰箱类电器营销亏损
B. 该公司2018年度小家电类电器营业收入和净利润相同
C. 该公司2018年度净利润主要由空调类电器销售提供
D. 剔除冰箱类电器销售数据后,该公司2018年度空调类电器销售净利润占比将会降低
【题目】诚信是立身之本,道德之基,某校学生会创设了“诚信水站”,既便于学生用水,又推进诚信教育,并用“![]() ”表示每周“水站诚信度”,为了便于数据分析,以四周为一周期,下表为该水站连续十二周(共三个周期)的诚信数据统计:
”表示每周“水站诚信度”,为了便于数据分析,以四周为一周期,下表为该水站连续十二周(共三个周期)的诚信数据统计:
第一周 | 第二周 | 第三周 | 第四周 | |
第一个周期 |
|
|
|
|
第二个周期 |
|
|
|
|
第三个周期 |
|
|
|
|
(1)计算表中十二周“水站诚信度”的平均数![]() ;
;
(2)分别从表中每个周期的4个数据中随机抽取1个数据,设随机变量![]() 表示取出的3个数中“水站诚信度”超过
表示取出的3个数中“水站诚信度”超过![]() 的数据的个数,求随机变量
的数据的个数,求随机变量![]() 的分布列和期望;
的分布列和期望;
(3)已知学生会分别在第一个周期的第四周末和第二个周期的第四周末各举行了一次“以诚为本”的主题教育活动,根据已有数据,说明两次主题教育活动的宣传效果,并根据已有数据陈述理由.