题目内容
18.已知α为锐角,向量$\overrightarrow{a}$=(cos(α-$\frac{π}{6}$),sin(α-$\frac{π}{6}$)),$\overrightarrow{b}$=($\sqrt{3}$,-1),且$\overrightarrow{a}•\overrightarrow{b}$=$\frac{2}{7}$.(1)若β为锐角,且cos(α+β)=-$\frac{11}{14}$,求角β;
(2)求$\frac{sin2α-2\sqrt{3}co{s}^{2}α}{1+cos2α}$的值.
分析 (1)利用向量的数量积得出2cosα=$\frac{2}{7}$,cos$α=\frac{1}{7}$,sin$α=\frac{4\sqrt{3}}{7}$,cos(α+β)=-$\frac{11}{14}$,β为锐角,sin(α+β)=整体求解cosβ=cos[(α+β)-α],即可得出角.
(2)tanα=4$\sqrt{3}$,利用公式化简得出$\frac{sin2α-2\sqrt{3}co{s}^{2}α}{1+cos2α}$=$\frac{2sinαcosα-2\sqrt{3}co{s}^{2}α}{2co{s}^{2}α}$=tanα$-\sqrt{3}$,即可求值.
解答 解:(1)∵向量$\overrightarrow{a}$=(cos(α-$\frac{π}{6}$),sin(α-$\frac{π}{6}$)),$\overrightarrow{b}$=($\sqrt{3}$,-1),且$\overrightarrow{a}•\overrightarrow{b}$=$\frac{2}{7}$.
∴$\sqrt{3}$cos($α-\frac{π}{6}$)-sin($α-\frac{π}{6}$)=$\frac{2}{7}$,即2cosα=$\frac{2}{7}$,cos$α=\frac{1}{7}$,sin$α=\frac{4\sqrt{3}}{7}$,
∵cos(α+β)=-$\frac{11}{14}$,β为锐角
∴sin(α+β)=$\frac{5\sqrt{3}}{14}$,
∵cosβ=cos[(α+β)-α]=(-$\frac{11}{14}$)×$\frac{1}{7}$+$\frac{5\sqrt{3}}{14}$×$\frac{4\sqrt{3}}{7}$=$\frac{49}{98}$=$\frac{1}{2}$,
∴β=60°,
(2)∵cos$α=\frac{1}{7}$,sin$α=\frac{4\sqrt{3}}{7}$,
∴tanα=4$\sqrt{3}$
∴$\frac{sin2α-2\sqrt{3}co{s}^{2}α}{1+cos2α}$=$\frac{2sinαcosα-2\sqrt{3}co{s}^{2}α}{2co{s}^{2}α}$=tanα$-\sqrt{3}$=4$\sqrt{3}-\sqrt{3}$=3$\sqrt{3}$.
点评 本题综合考查了三角变换,公式的运用,注意公式的灵活运用,角的整体变换,向量是经常与三角函数几何的题目,是高考常考的题目.

 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案| A. | 1 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -1 |
| A. | y=sin2x | B. | y=cosx | C. | y=sin($\frac{π}{2}$-2x) | D. | y=tanx |
| A. | A${\;}_{9}^{9}$A${\;}_{2}^{2}$ | B. | A${\;}_{9}^{9}$ | C. | A${\;}_{10}^{10}$ | D. | 2A${\;}_{10}^{9}$ |
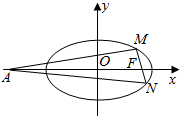 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,焦距为4,定点A(-4,0).
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,焦距为4,定点A(-4,0).