题目内容
【题目】已知![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]() ,若
,若![]() 且
且![]() 时,有
时,有![]() 成立.
成立.
(1)判断![]() 在
在![]() 上的单调性,并用定义证明;
上的单调性,并用定义证明;
(2)解不等式![]() ;
;
(3)若![]() 对所有的
对所有的![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() 或
或![]() 或
或![]()
【解析】
(1)利用函数单调性的定义,奇函数的性质,结合![]() ,判断
,判断![]() 在
在![]() 上的单调递增;
上的单调递增;
(2) 根据(1)的结论,以及函数的定义域,列出不等式组,求出x的范围;
(3)根据(1)的结论和条件,将问题转化为m2-2am+1≥1,即m2-2am≥0对a∈[-1,1]恒成立,构造函数g(a)= -2ma+m2,进而求得m的取值范围.
任取x1,x2∈[-1,1]且x1<x2,则-x2∈[-1,1],
∵f(x)为奇函数,∴f(-x2)= -f(x2),
∴f(x1)-f(x2)=f(x1)+f(-x2)=![]()
由已知得![]() >0,
>0,![]() <0,
<0,
∴f(x1)-f(x2)<0,即f(x1)<f(x2),∴f(x)在[-1,1]上单调递增.
(2)∵f(x)在[-1,1]上单调递增,∴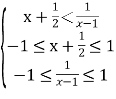 ,解得
,解得![]()
(3)∵f(1)=1,f(x)在[-1,1]上单调递增,∴在[-1,1]上,f(x)≤1.
问题转化为m2-2am+1≥1,即m2-2am≥0,对a∈[-1,1]恒成立.
设g(a)=-2m·a+m2.
①若m=0,则g(a)=0≥0,对a∈[-1,1]恒成立.
②若m≠0,则g(a)为a的一次函数,若g(a)≥0,对a∈[-1,1]恒成立,必须g(-1)≥0,且g(1)≥0,∴m≤-2或m≥2.
∴m的取值范围是m=0或m≤-2或m≥2.

 名校课堂系列答案
名校课堂系列答案【题目】第一次大考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于![]() 分为优秀,
分为优秀,![]() 分以下为非优秀,统计成绩后,得到如下
分以下为非优秀,统计成绩后,得到如下![]() 列联表,且已知在甲、乙两个文科班全部
列联表,且已知在甲、乙两个文科班全部![]() 人中随机抽取
人中随机抽取![]() 人为优秀的概率为
人为优秀的概率为![]() .
.
(I)请完成![]() 列联表:
列联表:
优秀 | 非优秀 | 合计 | |
甲班 |
| ||
乙班 |
| ||
合计 |
|
(Ⅱ)根据列联表的数据能否在犯错误的概率不超过![]() 的前提下认为成绩与班级有关系?
的前提下认为成绩与班级有关系?
参考公式和临界值表:
 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
