题目内容
双曲线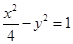
的顶点到其渐近线的距离等于____________.
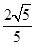
解析试题分析：不妨设顶点为
,一条渐近线为
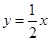即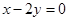
,点直线的距离为
.
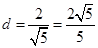考点：1、双曲线的性质；2、点到直线的距离.
练习册系列答案
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
题目内容
双曲线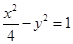的顶点到其渐近线的距离等于____________.
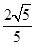
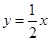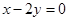解析试题分析：不妨设顶点为 ,一条渐近线为即,点直线的距离为.
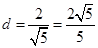考点：1、双曲线的性质；2、点到直线的距离.
同步轻松练习系列答案课课通课程标准思维方法与能力训练系列答案
，则其标准方程为_______.
的焦点且倾斜角为
的直线被圆
截得的弦长是__________．
是双曲线
的两个焦点，过点
的直线交双曲线
两点，若
为等边三角形，则双曲线
上的任意一点，若∠PF1F2=α，∠PF2F1=β，且cosα=
，sin(α+β)=
，则此椭圆的离心率为 ．
：
，
为坐标原点，
为
是
是等腰三角形，则
.
,F为抛物线
的焦点,动点
为抛物线上任意一点,当
取最小值时P的坐标为________．
的两条渐近线与抛物线
的准线分别交于
两点,
为坐标原点.若双曲线的离心率为2,
的面积为
,则
_________. 
＝1(a>0，b>0)的两个焦点，P是C上一点，若|PF1|＋|PF2|＝6a且△PF1F2的最小内角为30°，则双曲线C的离心率为________．