题目内容
已知抛物线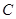 :
: ,
, 为坐标原点,
为坐标原点, 为
为 的焦点,
的焦点,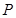 是
是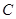 上一点. 若
上一点. 若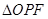 是等腰三角形,则
是等腰三角形,则 .
.
 或
或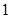
解析试题分析:由抛物线方程可知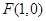 ,则
,则 。设点
。设点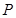 坐标为
坐标为 ,当
,当 时,由抛物线的定义可知
时,由抛物线的定义可知 ,则
,则 ,此时点
,此时点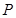 与原点重合故舍。当
与原点重合故舍。当 时,
时, 。当
。当 时,由抛物线的定义可知
时,由抛物线的定义可知 ,所以
,所以 ,解得
,解得 。所以
。所以 。综上可得
。综上可得
 或
或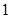 。
。
考点:1抛物线的定义;2抛物线的焦点坐标。

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
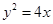 上的两点A、B满足
上的两点A、B满足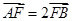 ,则弦AB的中点到准线的距离为____________.
,则弦AB的中点到准线的距离为____________. 的顶点到其渐近线的距离等于____________.
的顶点到其渐近线的距离等于____________.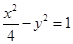 的顶点到其渐近线的距离等于____________.
的顶点到其渐近线的距离等于____________.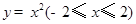 绕
绕 轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,该正方体的一个面恰好与旋转体的开口面平齐,则此正方体的体积是 .
轴旋转一周形成一个如图所示的旋转体,在此旋转体内水平放入一个正方体,该正方体的一个面恰好与旋转体的开口面平齐,则此正方体的体积是 .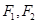 是双曲线
是双曲线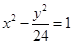 的两个焦点,
的两个焦点, 是双曲线与椭圆
是双曲线与椭圆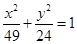 的一个公共点,则
的一个公共点,则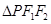 的面积等于_________.
的面积等于_________.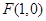 是抛物线
是抛物线 :
: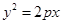 的焦点,则
的焦点,则 _______.
_______. 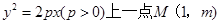 到其焦点的距离为5,双曲线
到其焦点的距离为5,双曲线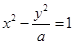 的左顶点为A,若双曲线一条渐近线与直线AM垂直,则实数a= .
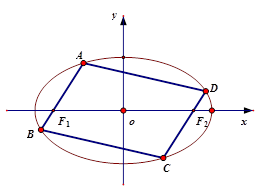
的左顶点为A,若双曲线一条渐近线与直线AM垂直,则实数a= .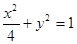 ,椭圆E的内接平行四边形的一组对边分别经过它的两个焦点(如图),则这个平行四边形面积的最大值是 .
,椭圆E的内接平行四边形的一组对边分别经过它的两个焦点(如图),则这个平行四边形面积的最大值是 .