题目内容
(本小题15分)已知动圆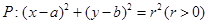 被y轴所截的弦长为2,被x轴分成两段弧,且弧长之比等于
被y轴所截的弦长为2,被x轴分成两段弧,且弧长之比等于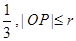 (其中
(其中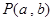 为圆心,O为坐标原点)。
为圆心,O为坐标原点)。
(1)求a,b所满足的关系式;
(2)点P在直线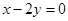 上的投影为A,求事件“在圆P内随机地投入一点,使这一点恰好在
上的投影为A,求事件“在圆P内随机地投入一点,使这一点恰好在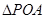 内”的概率的最大值
内”的概率的最大值
(1) 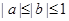 (2)
(2) 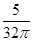
解析试题分析:(1)由题意知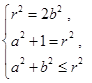
所以得到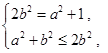 或者
或者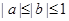
(2)点P到直线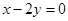 的距离
的距离
过点P且与直线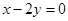 垂直的直线方程
垂直的直线方程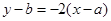
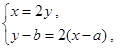 得出
得出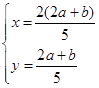
所以A点坐标是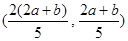 ,
,
所以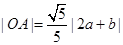
则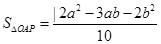 ,圆的面积是
,圆的面积是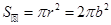
所以 。
。
令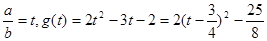 ,
,
因为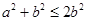 ,所以
,所以 ,
,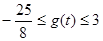
所以当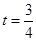 时,|
时,|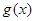 |取到最大值
|取到最大值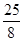 ,
,
即当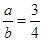 时,事件“在圆P内随机地投入一点,使这一点恰好落在
时,事件“在圆P内随机地投入一点,使这一点恰好落在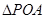 内”的概率的最大值为
内”的概率的最大值为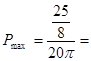
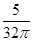 。
。
考点:几何概型
点评:解决的关键是理解线与圆的位置关系,结合面积比来求解概率的值,属于基础题。

练习册系列答案
相关题目
(本小题满分10分)某网站欲调查网民对当前网页的满意程度,在登录的所有网民中,收回有效帖子共50000份,其中持各种态度的份数如下表所示.
| 很满意 | 满意 | 一般 | 不满意 |
| 10800 | 12400 | 15600 | 11200 |
 的分布列,并求李明在一年内领到驾照的概率.
的分布列,并求李明在一年内领到驾照的概率. 。
。 层楼,写出
层楼,写出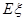 。
。 ,乙每次击中目标的概率为
,乙每次击中目标的概率为 ,两人间每次射击是否击中目标互不影响。
,两人间每次射击是否击中目标互不影响。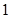 分,负者得
分,负者得 分,比赛进行到有一人比对方多
分,比赛进行到有一人比对方多 分或打满
分或打满 局时结束.假设选手甲与选手乙比赛时,甲每局获胜的概率皆为
局时结束.假设选手甲与选手乙比赛时,甲每局获胜的概率皆为 ,且各局比赛胜负互不影响.
,且各局比赛胜负互不影响. 局结束,且乙比甲多得
局结束,且乙比甲多得 表示比赛停止时已比赛的局数,求随机变量
表示比赛停止时已比赛的局数,求随机变量 为坐标原点,点
为坐标原点,点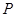 的坐标
的坐标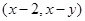
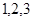 的三张卡片,现从此盒中有放回地先后抽到两张卡片的标号分别记为
的三张卡片,现从此盒中有放回地先后抽到两张卡片的标号分别记为 ,求|
,求| |的最大值,并求事件“|
|的最大值,并求事件“| ,
, ]上先后取两个数分别记为
]上先后取两个数分别记为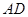 上取两点
上取两点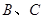 ,在
,在