题目内容
9.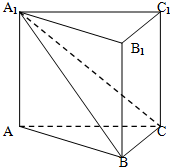 如图所示,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1,且AA1=AB=2.
如图所示,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1,且AA1=AB=2.(1)求证:AB⊥BC;
(2)若直线AC与平面A1BC所成的角的正弦值为$\frac{1}{2}$,求锐二面角A-A1C-B的大小.
分析 (1)取A1B的中点D,连接AD,由已知条件推导出AD⊥平面A1BC,从而AD⊥BC,由线面垂直得AA1⊥BC.由此能证明AB⊥BC.
(2)连接CD,由已知条件得∠ACD即为直线AC与平面A1BC所成的角,∠AED即为二面角A-A1C-B的一个平面角,由此能求出二面角A-A1C-B的大小.
解答  (1)证明:如图,取A1B的中点D,连接AD,
(1)证明:如图,取A1B的中点D,连接AD,
∵AA1=AB,∴AD⊥A1B,
∵平面A1BC⊥侧面A1ABB1,且平面A1BC∩侧面A1ABB1=A1B,
∴AD⊥平面A1BC,
又∵BC?平面A1BC,∴AD⊥BC,
∵三棱柱ABC---A1B1C1是直三棱柱,∴AA1⊥底面ABC,∴AA1⊥BC,
又AA1∩AD=A,从而BC⊥侧面A1ABB1,
又AB?侧面A1ABB1,故AB⊥BC;
(2)解:连接CD,由(1)可知AD⊥平面A1BC,
则CD是AC在平面A1BC内的射影,
∴∠ACD即为直线AC与平面A1BC所成的角,
又∵sin∠ACD=$\frac{1}{2}$,∴∠ACD=$\frac{π}{6}$,
∵在等腰直角△A1AB中,AA1=AB=2,且点D是A1B中点,
∴AD=$\frac{1}{2}$A1B=$\sqrt{2}$,且∠ADC=$\frac{π}{2}$,
∴AC=2$\sqrt{2}$,
过点A作AE⊥A1C于点E,连DE,
由(1)知AD⊥平面A1BC,则AD⊥A1C,且AE∩AD=A,
∴∠AED即为二面角A-A1C-B的一个平面角,
且直角△A1AC中:AE=$\frac{{A}_{1}A•AC}{{A}_{1}C}$=$\frac{2×2\sqrt{2}}{2\sqrt{3}}$=$\frac{2\sqrt{6}}{3}$,
又AD=$\sqrt{2}$,∠ADE=$\frac{π}{2}$,
∴sin∠AED=$\frac{AD}{AE}$=$\frac{\sqrt{2}}{\frac{2\sqrt{6}}{3}}$=$\frac{\sqrt{3}}{2}$,且二面角A-A1C-B为锐二面角,
∴∠AED=$\frac{π}{3}$,即二面角A-A1C-B的大小为$\frac{π}{3}$.
点评 本题考查异面直线垂直的证明,考查二面角的大小的求法,解题时要认真审题,注意空间思维能力的培养,注意解题方法的积累,属于中档题.

 如图,在多面体ABCDEF中,平面ADEF⊥平面ABCD,AB∥DC,ADEF是正方形,已知BD=2AD=2,AB=2DC=$\sqrt{5}$.
如图,在多面体ABCDEF中,平面ADEF⊥平面ABCD,AB∥DC,ADEF是正方形,已知BD=2AD=2,AB=2DC=$\sqrt{5}$. 已知四边形ABCD为平行四边形,BC⊥平面ABE,AE⊥BE,BE=BC=1,AE=$\sqrt{3}$,M为线段AB的中点,N为线段DE的中点,P为线段AE的中点.
已知四边形ABCD为平行四边形,BC⊥平面ABE,AE⊥BE,BE=BC=1,AE=$\sqrt{3}$,M为线段AB的中点,N为线段DE的中点,P为线段AE的中点. 如图,某快递公司送货员从公司A处准备开车送货到某单位B处,有A→C→D→B,A→E→F→B两条路线.若该地各路段发生堵车与否是相互独立的,且各路段发生堵车事件的概率如图所示(例如A→C→D算作两个路段;路段AC发生堵车事件的概率为$\frac{1}{6}$,路段CD发生堵车事件的概率为$\frac{1}{10}$).
如图,某快递公司送货员从公司A处准备开车送货到某单位B处,有A→C→D→B,A→E→F→B两条路线.若该地各路段发生堵车与否是相互独立的,且各路段发生堵车事件的概率如图所示(例如A→C→D算作两个路段;路段AC发生堵车事件的概率为$\frac{1}{6}$,路段CD发生堵车事件的概率为$\frac{1}{10}$). 在长方体ABCD-A1B1C1D1中,AA1=9,AB=BC=6$\sqrt{3}$,N,M,P分别为BC,A1B1,C1D1的中点.
在长方体ABCD-A1B1C1D1中,AA1=9,AB=BC=6$\sqrt{3}$,N,M,P分别为BC,A1B1,C1D1的中点.