题目内容
18.已知直线ax+by+c=0在x,y轴上的截距分别是-3和4,则直线方程为4x-3y+12=0.分析 直接写出直线方程的截距式,然后化为一般式得答案.
解答 解:∵直线ax+by+c=0在x,y轴上的截距分别是-3和4,
∴由直线方程的截距式得直线方程为:$\frac{x}{-3}+\frac{y}{4}=1$,
化为一般式得:4x-3y+12=0.
故答案为:4x-3y+12=0.
点评 本题考查了直线方程的截距式,是基础题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
6. 一个大风车的半径为8m,12min旋转一周,它的最低点Po离地面2m,风车翼片的一个端点P从Po开始按逆时针方向旋转,则点P离地面距离h(m)与时间f(min)之间的函数关系式是( )
一个大风车的半径为8m,12min旋转一周,它的最低点Po离地面2m,风车翼片的一个端点P从Po开始按逆时针方向旋转,则点P离地面距离h(m)与时间f(min)之间的函数关系式是( )
 一个大风车的半径为8m,12min旋转一周,它的最低点Po离地面2m,风车翼片的一个端点P从Po开始按逆时针方向旋转,则点P离地面距离h(m)与时间f(min)之间的函数关系式是( )
一个大风车的半径为8m,12min旋转一周,它的最低点Po离地面2m,风车翼片的一个端点P从Po开始按逆时针方向旋转,则点P离地面距离h(m)与时间f(min)之间的函数关系式是( )| A. | $h(t)=-8sin\frac{π}{6}t+10$ | B. | $h(t)=-8cos\frac{π}{6}t+10$ | C. | $h(t)=-8sin\frac{π}{6}t+8$ | D. | $h(t)=-8cos\frac{π}{6}t+8$ |
13. 某几何体的三视图如图所示,正视图,侧视图,俯视图都是边长为1的正方形,则此几何体的外接球和内接球的半径分别为( )
某几何体的三视图如图所示,正视图,侧视图,俯视图都是边长为1的正方形,则此几何体的外接球和内接球的半径分别为( )
 某几何体的三视图如图所示,正视图,侧视图,俯视图都是边长为1的正方形,则此几何体的外接球和内接球的半径分别为( )
某几何体的三视图如图所示,正视图,侧视图,俯视图都是边长为1的正方形,则此几何体的外接球和内接球的半径分别为( )| A. | $\frac{\sqrt{3}}{2}$,$\frac{\sqrt{3}}{6}$ | B. | $\frac{\sqrt{3}}{2}$,$\frac{\sqrt{6}}{12}$ | C. | $\frac{\sqrt{6}}{4}$,$\frac{\sqrt{6}}{12}$ | D. | $\frac{\sqrt{6}}{4}$,$\frac{\sqrt{3}}{6}$ |
10.已知f(x)=ax+1的反函数经过(3,1),则f(2)=( )
| A. | 1 | B. | 3 | C. | 5 | D. | 9 |
5.在某次数学测试中,记答对题数:大于或等于6道为合格,小于6道为不合格,现从A,B两个班级随机抽取5人答对的题数进行分析,结果记录如下:
由于表格受损,数据m,n看不清,统计人员只记得m<n,且在抽取的数据中,A班的平均数比B班的平均数多1道题,两班数据的方差相同
(1)求表格中m和n的值;
(2)若从抽取的B班5人中任取2人,求2人都合格的概率.
| A班 | 5 | 5 | 8 | 8 | 9 |
| B班 | m | 4 | 7 | n | 8 |
(1)求表格中m和n的值;
(2)若从抽取的B班5人中任取2人,求2人都合格的概率.
6.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的实轴长为2,离心率为$\sqrt{5}$,则它的一个焦点到它的一条渐近线的距离为( )
| A. | 1 | B. | 2 | C. | $\sqrt{5}$ | D. | 2$\sqrt{2}$ |
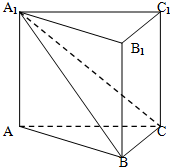 如图所示,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1,且AA1=AB=2.
如图所示,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1,且AA1=AB=2.