题目内容
17. 已知四边形ABCD为平行四边形,BC⊥平面ABE,AE⊥BE,BE=BC=1,AE=$\sqrt{3}$,M为线段AB的中点,N为线段DE的中点,P为线段AE的中点.
已知四边形ABCD为平行四边形,BC⊥平面ABE,AE⊥BE,BE=BC=1,AE=$\sqrt{3}$,M为线段AB的中点,N为线段DE的中点,P为线段AE的中点.(1)求证:MN⊥EA;
(2)求二面角M-NE-A的余弦值.
分析 (1)过B作BQ⊥平面ABCD,以B为原点,以BA、BC、BQ分别为x、y、z轴建立空间直角坐标系,证明$\overrightarrow{MN}$•$\overrightarrow{AE}$=0即可;
(2)所求值即为平面MNE的法向量与平面ANE的法向量的夹角的余弦值的绝对值,计算即可.
解答  (1)证明:∵BC⊥平面ABE,BC?平面ABCD,
(1)证明:∵BC⊥平面ABE,BC?平面ABCD,
∴平面ABE⊥平面ABCD,BC⊥AB,
过B作BQ⊥平面ABCD,则BQ?平面ABE,
以B为原点,以BA、BC、BQ分别为x、y、z轴建立空间直角坐标系如图,
∵AE⊥BE,BE=1,AE=$\sqrt{3}$,
∴AB=$\sqrt{A{E}^{2}+B{E}^{2}}$=2,
∴A(2,0,0),B(0,0,0),
∴M(1,0,0),D(2,1,0),E($\frac{1}{2}$,0,$\frac{\sqrt{3}}{2}$),N($\frac{5}{4}$,$\frac{1}{2}$,$\frac{\sqrt{3}}{4}$),
∴$\overrightarrow{MN}$=($\frac{1}{4}$,$\frac{1}{2}$,$\frac{\sqrt{3}}{4}$),$\overrightarrow{AE}$=(-$\frac{3}{2}$,0,$\frac{\sqrt{3}}{2}$),
∵$\overrightarrow{MN}$•$\overrightarrow{AE}$=$-\frac{3}{8}+0+\frac{3}{8}$=0,
∴MN⊥EA;
(2)解:由(1)得:$\overrightarrow{MN}$=($\frac{1}{4}$,$\frac{1}{2}$,$\frac{\sqrt{3}}{4}$),$\overrightarrow{NE}$=(-$\frac{3}{4}$,-$\frac{1}{2}$,$\frac{\sqrt{3}}{4}$),
$\overrightarrow{AN}$=(-$\frac{3}{4}$,$\frac{1}{2}$,$\frac{\sqrt{3}}{4}$),$\overrightarrow{AE}$=(-$\frac{3}{2}$,0,$\frac{\sqrt{3}}{2}$),
设平面MNE的法向量为$\overrightarrow{n}$=(x,y,z),
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{MN}=0}\\{\overrightarrow{n}•\overrightarrow{NE}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{\frac{1}{4}x+\frac{1}{2}y+\frac{\sqrt{3}}{4}z=0}\\{-\frac{3}{4}x-\frac{1}{2}y+\frac{\sqrt{3}}{4}z=0}\end{array}\right.$,
取x=1,得$\overrightarrow{n}$=(1,-1,$\frac{\sqrt{3}}{3}$),
设平面ANE的法向量为$\overrightarrow{m}$=(x,y,z),
由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AN}=0}\\{\overrightarrow{m}•\overrightarrow{AE}=0}\end{array}\right.$,得$\left\{\begin{array}{l}{-\frac{3}{4}x+\frac{1}{2}y+\frac{\sqrt{3}}{4}z=0}\\{-\frac{3}{2}x+\frac{\sqrt{3}}{2}z=0}\end{array}\right.$,
取x=1,得$\overrightarrow{m}$=(1,0,$\sqrt{3}$),
∴$cos<\overrightarrow{m},\overrightarrow{n}>$=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$=$\frac{1+0+1}{\sqrt{1+1+\frac{1}{3}}•\sqrt{1+3}}$=$\frac{\sqrt{21}}{7}$,
∴所求二面角M-NE-A的余弦值为$\frac{\sqrt{21}}{7}$.
点评 本题考查线面垂直的位置关系,二面角,数量积运算,解决的关键是利用向量的数量积公式以及线面垂直的性质定理得到证明,注意解题方法的积累,属于中档题.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案 一个大风车的半径为8m,12min旋转一周,它的最低点Po离地面2m,风车翼片的一个端点P从Po开始按逆时针方向旋转,则点P离地面距离h(m)与时间f(min)之间的函数关系式是( )
一个大风车的半径为8m,12min旋转一周,它的最低点Po离地面2m,风车翼片的一个端点P从Po开始按逆时针方向旋转,则点P离地面距离h(m)与时间f(min)之间的函数关系式是( )| A. | $h(t)=-8sin\frac{π}{6}t+10$ | B. | $h(t)=-8cos\frac{π}{6}t+10$ | C. | $h(t)=-8sin\frac{π}{6}t+8$ | D. | $h(t)=-8cos\frac{π}{6}t+8$ |
| A班 | 5 | 5 | 8 | 8 | 9 |
| B班 | m | 4 | 7 | n | 8 |
(1)求表格中m和n的值;
(2)若从抽取的B班5人中任取2人,求2人都合格的概率.
 已知点P(c,$\frac{3}{2}$c)在以F(c,0)为右焦点的椭圆Γ:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,斜率为l的直线m过点F与椭圆Γ交于A,B两点,且与直线l:x=4c交于点M,求椭圆Γ的离心率e.
已知点P(c,$\frac{3}{2}$c)在以F(c,0)为右焦点的椭圆Γ:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,斜率为l的直线m过点F与椭圆Γ交于A,B两点,且与直线l:x=4c交于点M,求椭圆Γ的离心率e.
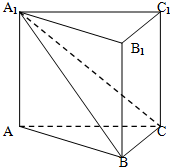 如图所示,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1,且AA1=AB=2.
如图所示,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1,且AA1=AB=2.