题目内容
2.设A、B、C、D是球面上的四个点,且在同一平面内,AB=BC=CD=DA=1,球心到该平面的距离是球半径的$\frac{\sqrt{3}}{2}$倍,则球的体积是$\frac{8\sqrt{2}π}{3}$.分析 设出球的半径,球心到该平面的距离是球半径的$\frac{\sqrt{3}}{2}$倍,结合ABCD的对角线的一半,满足勾股定理,求出R即可求球的体积.
解答 解:设球的半径为R,由题意可得$(\frac{\sqrt{2}}{2})^{2}+(\frac{\sqrt{3}}{2}R)^{2}={R}^{2}$
∴R=$\sqrt{2}$,
∴球的体积是:$\frac{4π}{3}•(\sqrt{2})^{3}$=$\frac{8\sqrt{2}π}{3}$.
故答案为:$\frac{8\sqrt{2}π}{3}$.
点评 本题考查球的体积,考查空间想象能力,计算能力,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知点P(c,$\frac{3}{2}$c)在以F(c,0)为右焦点的椭圆Γ:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,斜率为l的直线m过点F与椭圆Γ交于A,B两点,且与直线l:x=4c交于点M,求椭圆Γ的离心率e.
已知点P(c,$\frac{3}{2}$c)在以F(c,0)为右焦点的椭圆Γ:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上,斜率为l的直线m过点F与椭圆Γ交于A,B两点,且与直线l:x=4c交于点M,求椭圆Γ的离心率e.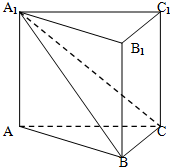 如图所示,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1,且AA1=AB=2.
如图所示,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1,且AA1=AB=2.