题目内容
14.已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一焦点F在抛物线y2=4x的准线上,且点M(1,-$\frac{\sqrt{2}}{2}$)在椭圆上.(Ⅰ)求椭圆E的方程;
(Ⅱ)过直线x=-2上一点P作椭圆E的切线,切点为Q,证明:PF⊥QF.
分析 (1)根据抛物线方程求出其准线,确定焦点的坐标,然后求出椭圆中的c,再根据M点在椭圆上,求出椭圆方程;
(2)设出PQ直线方程,然后与椭圆方程联立,根据△=0,求出P、Q坐标,然后证明平面向量的数量积为0,即表示PF⊥QF.
解答 (本小题满分13分)
解:(Ⅰ)抛物线y2=4x的准线为x=-1,则F(-1,0),c=1.…(2分)
又M(1,-$\frac{\sqrt{2}}{2}$)在椭圆上,则$\frac{1}{{a}^{2}}+\frac{1}{2({a}^{2}-1)}=1$,解得a2=2,…(4分)
故椭E的方程$\frac{{x}^{2}}{2}+{y}^{2}=1$.…(5分)
(Ⅱ)设P(-2,y0)、Q(x1,y1).
依题意可知切线PQ的斜率存在,设为k,PQ:y=kx+m,并代入方程$\frac{{x}^{2}}{2}+{y}^{2}=1$中,
整理得:(2k2+1)x2+4mkx+2(m2-1)=0…(8分)
因△=16m2k2-8(2k2+1)(m2-1)=0,即m2=2k2+1.…(9分)
从而${x}_{1}=-\frac{2mk}{2{k}^{2}+1}$,${y}_{1}=\frac{m}{2{k}^{2}+1}$所以Q(-$\frac{2mk}{2{k}^{2}+1}$,$\frac{m}{2{k}^{2}+1}$);…(10分)
又y0=-2k+m,则P(-2,-2k+m),$\overrightarrow{PF}$=(1,2k-m)$\overrightarrow{QF}$=($\frac{2mk}{2{k}^{2}+1}$-1,-$\frac{m}{2{k}^{2}+1}$).…(11分)
由于$\overrightarrow{PF}•\overrightarrow{QF}$=$\frac{2mk}{2{k}^{2}+1}$-1-$\frac{m(2k-m)}{2{k}^{2}+1}$=$\frac{{m}^{2}}{2{k}^{2}+1}-1=0$,故PF⊥QF.…(13分)
点评 本题考查了椭圆和抛物线的标准方程,同时与平面向量的知识结合考查学生的运算能力,本题对学生的计算能力要求较高.

 一个大风车的半径为8m,12min旋转一周,它的最低点Po离地面2m,风车翼片的一个端点P从Po开始按逆时针方向旋转,则点P离地面距离h(m)与时间f(min)之间的函数关系式是( )
一个大风车的半径为8m,12min旋转一周,它的最低点Po离地面2m,风车翼片的一个端点P从Po开始按逆时针方向旋转,则点P离地面距离h(m)与时间f(min)之间的函数关系式是( )| A. | $h(t)=-8sin\frac{π}{6}t+10$ | B. | $h(t)=-8cos\frac{π}{6}t+10$ | C. | $h(t)=-8sin\frac{π}{6}t+8$ | D. | $h(t)=-8cos\frac{π}{6}t+8$ |
| X | 0 | 1 |
| P | $\frac{a}{2}$ | $\frac{{a}^{2}}{2}$ |
| A. | 2 | B. | 2或$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |

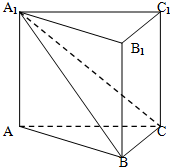 如图所示,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1,且AA1=AB=2.
如图所示,在直三棱柱ABC-A1B1C1中,平面A1BC⊥侧面A1ABB1,且AA1=AB=2.