题目内容
6.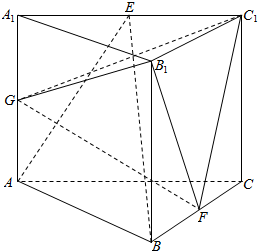 在直三棱柱ABC-A1B1C1中,AC=4,CB=AA1=2,AB=2$\sqrt{3}$ E,F,G分别是A1C1,BC,AA1的中点.
在直三棱柱ABC-A1B1C1中,AC=4,CB=AA1=2,AB=2$\sqrt{3}$ E,F,G分别是A1C1,BC,AA1的中点.(1)证明:平面AEB⊥平面BB1CC1
(2)证明:C1F∥平面ABE
(3)求三棱锥C1-B1GF的体积.
分析 (1)由直三棱柱ABC-A1B1C1得B1B⊥平面ABC,从而有B1B⊥BC,由AB,BC,AC的长度可得AB⊥BC,可证AB⊥平面B1BC,推出平面AEB⊥平面BB1C1C;
(2)取AB中点D,连结DF,DE,由中位线定理可得DF∥AC,DF=$\frac{1}{2}$AC,又因为EC1∥AC,EC1=$\frac{1}{2}$AC,故而四边形EDFC1是平行四边形,所以C1F∥DE,推出C1F∥平面ABE
(3)取B1B中点M,B1C1中点N,连结GM,FN,则GM⊥平面BB1C1C,即GM为棱锥的高,底面B1C1F是等腰三角形,代入体积公式计算即可.
解答 证明:(1)∵三棱柱ABC-A1B1C1是直三棱柱,
∴B1B⊥平面ABC,∵BC?平面ABC,
∴B1B⊥BC,
∵AC=4,CB=2,AB=2$\sqrt{3}$,
∴BC2+AB2=AC2,即AB⊥BC,
又∵B1B?平面面BB1C1C,BC?平面BB1C1C,B1B∩BC=B,
∴AB⊥平面BB1C1C,∵AB?平面AEB,
∴平面AEB⊥平面BB1C1C.
(2)取AB中点D,连结DF,DE,
则DF是△ABC的中位线,∴DF∥AC,DF=$\frac{1}{2}$AC,
∵四边形A1ACC1是平行四边形,E是A1C1的中点,
∴EC1∥AC,EC1=$\frac{1}{2}$AC,
∴EC1∥DF,EC1=DF,
∴四边形EDFC1是平行四边形,
∴C1F∥DE,∵DE?平面ABE,C1F?平面ABE,
∴C1F∥平面ABE.
(3)取B1B中点M,B1C1中点N,连结GM,FN,
则GM∥AB,GM=AB=2$\sqrt{3}$,FN⊥B1C1,FN=A1A=2,B1C1=BC=2
∵AB⊥平面BB1C1C,
∴GM⊥平面BB1C1C,
∴V${\;}_{棱锥{C}_{1}-{B}_{1}GF}$=V${\;}_{棱锥G-{B}_{1}{C}_{1}F}$=$\frac{1}{3}$•S${\;}_{△{B}_{1}{C}_{1}F}$•GM=$\frac{1}{3}$•$\frac{1}{2}$•B1C1•FN•GM=$\frac{1}{3}$$•\frac{1}{2}$•2•2•2$\sqrt{3}$=$\frac{4\sqrt{3}}{3}$.
点评 本题考查了线面平行,面面垂直的判定和几何体体积,构造平行线和垂线是解题关键.

 导学全程练创优训练系列答案
导学全程练创优训练系列答案
| A. | 2.3 | B. | 2.4 | C. | 2.5 | D. | 2.6 |
| A. | 数据5,4,4,3,5,2的众数是4 | |
| B. | 根据样本估计总体,其误差与所选择的样本容量无关 | |
| C. | 数据2,3,4,5的标准差是数据4,6,8,10的标准差的一半 | |
| D. | 频率分布直方图中各小长方形的面积等于相应各组的频数 |
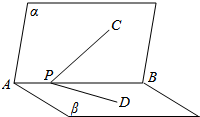 如图,平面α⊥平面β,平面α∩平面β=AB,P∈AB,C∈α,D∈β,且∠CPB=∠DPB=45°,则∠CPD=60°.
如图,平面α⊥平面β,平面α∩平面β=AB,P∈AB,C∈α,D∈β,且∠CPB=∠DPB=45°,则∠CPD=60°.