题目内容
11.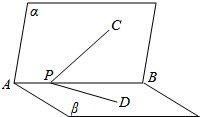 如图,平面α⊥平面β,平面α∩平面β=AB,P∈AB,C∈α,D∈β,且∠CPB=∠DPB=45°,则∠CPD=60°.
如图,平面α⊥平面β,平面α∩平面β=AB,P∈AB,C∈α,D∈β,且∠CPB=∠DPB=45°,则∠CPD=60°.
分析 作CO⊥AB,交AB于O,在平面β内作OD⊥AB,交PD于点D,连结CD,由已知推导出△COP,△DOP,△COD是全等的等腰直角三角形,由此能求出∠CPD.
解答  解:作CO⊥AB,交AB于O,在平面β内作OD⊥AB,交PD于点D,连结CD,
解:作CO⊥AB,交AB于O,在平面β内作OD⊥AB,交PD于点D,连结CD,
∵平面α⊥平面β,平面α∩平面β=AB,P∈AB,C∈α,D∈β,且∠CPB=∠DPB=45°,
∴∠COD是二面角α-AB-β的平面角,∴∠COD=90°,
∴△COP,△DOP,△COD是全等的等腰直角三角形,
∴PC=PD=CD,
∴∠CPD=60°.
故答案为:60°.
点评 本题考查角的大小的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
1.已知全集U=R,集合A={x|x+1<0},B={x|x2+3x<0},则 (∁UA)∩B等于( )
| A. | {x|-3<x<0} | B. | {x|-1≤x<0} | C. | {x|x<-1} | D. | {x|-1<x<0} |
16.小颖看到一卷卫生纸上标明了重量,她想验证一下,就来到物理实验室,用天平称后,正好是180克.接下来她又想知道这卷卫生纸的长度和单层卫生纸的厚度,但又不想将卫生纸全都展开.请你利用物理实验室和包装上的信息,为小颖设计一种实现想法的方案.
| 产品名称:180克维达卫生纸 |
| 产品编号:v4131 |
| 主要原料:100%原生木浆 |
| 执行标准:GB20810 优等品(合格) |
| 生产日期:见包装 保质期:三年 |
| 规格:3层 138mm×104mm/节 净含量:180克 |
 在直三棱柱ABC-A1B1C1中,AC=4,CB=AA1=2,AB=2$\sqrt{3}$ E,F,G分别是A1C1,BC,AA1的中点.
在直三棱柱ABC-A1B1C1中,AC=4,CB=AA1=2,AB=2$\sqrt{3}$ E,F,G分别是A1C1,BC,AA1的中点.