题目内容
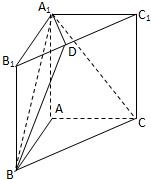
如图, 在直三棱柱ABC－A1B1C1中，AC＝3，BC＝4，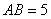
,
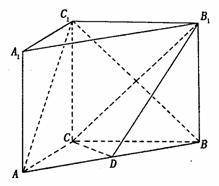AA1＝4，点D是AB的中点， (I）求证：AC⊥BC1；
(II）求证：AC 1//平面CDB1；
【答案】
解 ：（I）直三棱柱ABC－A1B1C1，底面三边长AC=3，BC=4AB=5，
∴ AC⊥BC，又 AC⊥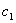
C，∴ AC⊥平面BCC1；
∴ AC⊥BC1
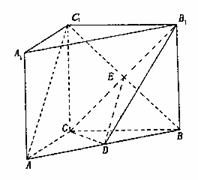
(II）设CB1与C1B的交点为E，连结DE，
∵ D是AB的中点，E是BC1的中点，∴ DE//AC1，
∵ DE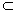
平面CDB1，AC1
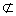平面CDB1，
∴ AC1//平面CDB1；
练习册系列答案
期末集结号系列答案
相关题目
如图，在直三棱柱ABC-A1B1C1中，∠BAC=90°，AB=a，AC=2，AA1=1，点D在棱B1C1上且B1D：DC1=1：3
如图，在直三棱柱ABC-A1B1C1中，∠ABC=90°，AB=BC=AA1=2，D是AB的中点．
如图，在直三棱柱ABC-A1B1C1中，∠ACB=90°，AC=BC=CC1=a，E是A1C1的中点，F是AB中点．
如图：在直三棱柱ABC-DEF中，AB=2，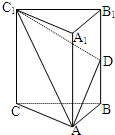
如图，在直三棱柱ABC-A1B1C1中，