题目内容
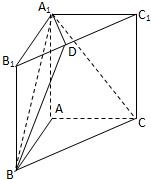 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=a,AC=2,AA1=1,点D在棱B1C1上且B1D:DC1=1:3
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=a,AC=2,AA1=1,点D在棱B1C1上且B1D:DC1=1:3(1)证明:无论a为任何正数,均有BD⊥A1C;
(2)当a为何值时,二面角B-A1D-B1为60°.
分析:(1)由题意建立如图示的空间直角坐标系,学出各个点的坐标进利用向量的垂直证明了线线的垂直;
(2)利用方程的思想,先设出未知的变量,利用两个平面的法向量与平面所成的二面角的大小之间的关系建立方程进行求出变量的数值.
(2)利用方程的思想,先设出未知的变量,利用两个平面的法向量与平面所成的二面角的大小之间的关系建立方程进行求出变量的数值.
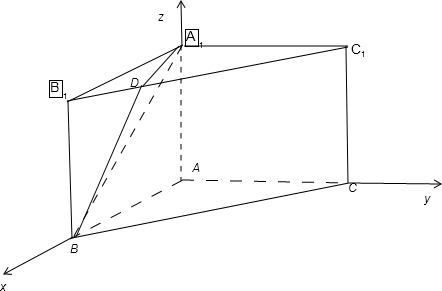
解答:解:(1)以A为坐标原点,建立空间直角坐标系A-xyz(如图),
D(
a,
,1),A1(0,0,1),B(a,0,0),C(0,2,0),
=(-
,
,1),
=(0,2,-1),
∵
•
=(-
,
,1)•(0,2,-1)=0,∴
⊥
,即BD⊥A1C.
故无论a为任何正数,均有BD⊥A1C.
(2)
=(
a,
,0),
=(a,0,-1),
设平面A1BD的一个法向量为
=(x,y,z),则
⊥
,
⊥
,
故
,即
,取
=(
,-
,1).
又平面A1B1D的一个法向量为
=(0,0,1)
∴cos?
,
>=
=
=
,
结合图形知?
,
>与二面角B-A1D-B1相等,即?
,
>=60°,
∴
=
,
解得a=
,
故当a=
时,二面角B-A1D-B1为60°.

D(
| 3 |
| 4 |
| 1 |
| 2 |
| BD |
| a |
| 4 |
| 1 |
| 2 |
| A1C |
∵
| BD |
| A1C |
| a |
| 4 |
| 1 |
| 2 |
| BD |
| A1C |
故无论a为任何正数,均有BD⊥A1C.
(2)
| A1D |
| 3 |
| 4 |
| 1 |
| 2 |
| A1B |
设平面A1BD的一个法向量为
| n |
| n |
| A1D |
| n |
| A1B |
故
|
|
| n |
| 1 |
| a |
| 3 |
| 2 |
又平面A1B1D的一个法向量为
| m |
∴cos?
| m |
| n |
| ||||
|
|
| 1 | ||||||
|
| 1 | ||||||
|
结合图形知?
| m |
| n |
| m |
| n |
∴
| 1 | ||||||
|
| 1 |
| 2 |
解得a=
2
| ||
| 3 |
故当a=
2
| ||
| 3 |
点评:此题重点考查了利用空间向量的坐标表示法内容解决线线垂直的证明,还考查了二面角的大小与平面的法向量夹角之间的关系及利用方程的思想求解的方法.

练习册系列答案
相关题目




