题目内容
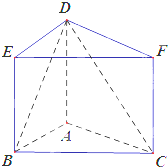 如图:在直三棱柱ABC-DEF中,AB=2,AC=AD=2
如图:在直三棱柱ABC-DEF中,AB=2,AC=AD=2| 3 |
(1)证明:AB⊥DC,
(2)求二面角A-DC-B的余弦值.
分析:(1)利用直棱柱的性质和线面垂直的判定和性质定理即可证明;
(2)利用线面垂直的性质、正方形的性质、三垂线定理、二面角的定义即可得出.
(2)利用线面垂直的性质、正方形的性质、三垂线定理、二面角的定义即可得出.
解答:解:(1)在直三棱柱ABC-DEF中,则AD⊥AB,
又∵AB⊥AC,AD∩AC=A.
∴AB⊥平面ACFD,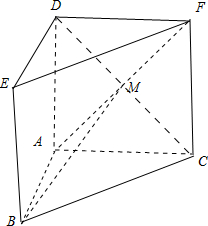
∴AB⊥CD.
(2)由(1)可得:四边形ACFD为正方形,
连接对角线AF、CD相较于点M,则AM⊥CD.
又∵AB⊥平面ACFD,根据三垂线定理可得CD⊥BM.
∴∠AMB是二面角A-DC-B的平面角.
∵AM=
×2
×
=
,∴BM=
=
=
..
∴在Rt△ABM中,cos∠AMB=
=
=
.
故二面角A-DC-B的余弦值为
.
又∵AB⊥AC,AD∩AC=A.
∴AB⊥平面ACFD,

∴AB⊥CD.
(2)由(1)可得:四边形ACFD为正方形,
连接对角线AF、CD相较于点M,则AM⊥CD.
又∵AB⊥平面ACFD,根据三垂线定理可得CD⊥BM.
∴∠AMB是二面角A-DC-B的平面角.
∵AM=
| 1 |
| 2 |
| 3 |
| 2 |
| 6 |
| AB2+AM2 |
22+(
|
| 10 |
∴在Rt△ABM中,cos∠AMB=
| AM |
| BM |
| ||
|
| ||
| 10 |
故二面角A-DC-B的余弦值为
| ||
| 10 |
点评:熟练掌握棱柱的性质和线面垂直的判定和性质定理、正方形的性质、三垂线定理、二面角的定义是解题的关键.

练习册系列答案
相关题目




