Question

如图，在直三棱柱ABC-A₁B₁C₁中，A1A=AC=

2

AB，AB=BC=a，D为BB₁的中点．
（1）证明：平面ADC₁⊥平面ACC₁A₁；
（2）求平面ADC₁与平面ABC所成的二面角大小．

Answer 1

分析：（1）以B为坐标原点建立空间坐标系，分析求出向量

DE

，

AC1

，

CC1

的坐标，进而根据

DE

•

AC1

=0，

DE

•

CC1

=0，结合线面垂直的判定定理得到DE⊥面A₁ACC₁，再由面面垂直的判定定理即可得到平面ADC₁⊥面A₁ACC₁．
（2）求出平面ADC₁与平面ABC的法向量坐标，代入向量夹角公式，求出平面ADC₁与平面ABC所成的二面角的余弦值，进而可以求出平面ADC₁与平面ABC所成的二面角．

解答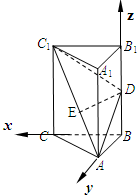：解：由勾股定理知，AB⊥BC，则如图所示建立直角坐标系，坐标分别为：
B（0，0，0），A（0，a，0），C（a，0，0），B₁（0，0，

2

a)，A1(0，a，

2

a）C₁（a，0，

2

a）
（1）∵D₁，E分别是BB₁，AC₁之中点．
∴D（0，0，

2

2

a)，E(

a

2

，

a

2

，

2

2

故

DE

=(

a

2

，

a

2

，0)，

CC1

=(0，0，

2

a)，

AC1

=(a，-a，

2

a）
∵

DE

•

AC1

=0，

DE

•

CC1

=0，
∴DE⊥面A₁ACC₁，∴平面ADC₁⊥面A₁ACC₁．…（6分）
（2）显然平面ABC的法向量为

m

=（0，0，1），
设平面ADC₁的法向量

n

=(x1，y1，z1），且

AD

=(0，-a，

2

2

a)，

AC1

=(a，-a，

2

a）
令

AD • n =0 AC1 • n =0

⇒

n

=(-

2

2

，

2

2

，1），…（8分）
∴cos＜

m，

n

＞=

1

1 2 + 1 2 +1 •1

=

1

2

=

2

2

，
故两平面的夹角为

π

4

…（12分）

点评：本题考查的知识点是用空间向量求平面间的夹角，平面与平面垂直的判定，其中建立空间坐标系，将空间线面关系判定及二面角问题转化为向量夹角问题是解答本题的关键．