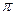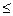题目内容
函数f(x)=3sin(2x-
)的图象为C,下列命题:
①图象C关于直线x=
π对称;
②函数f(x)在区间(-
,
)内是增函数;
③将y=sin(2x-
)的图象上的点横坐标保持不变,纵坐标变为原来的3倍即可得到图象C;
④图象C关于点(
,0)对称.
其中,正确命题的编号是______.(写出所有正确命题的编号)
| π |
| 3 |
①图象C关于直线x=
| 11 |
| 12 |
②函数f(x)在区间(-
| π |
| 12 |
| 5π |
| 12 |
③将y=sin(2x-
| π |
| 3 |
④图象C关于点(
| π |
| 3 |
其中,正确命题的编号是______.(写出所有正确命题的编号)
∵函数f(x)=3sin(2x-
)的图象为C,当x=
π时,f(x)=3sin
=-3,取得最小值,故①图象C关于直线x=
π对称,故①正确.
令 2kπ-
≤2x-
≤2kπ+
,求得kπ-
≤x≤kπ+
,k∈z,故函数的增区间为[-
,kπ+
],k∈z,
故f(x)在区间(-
,
)内是增函数,故②正确.
将y=sin(2x-
)的图象上的点横坐标保持不变,纵坐标变为原来的3倍即可得到f(x)=3sin(2x-
)的图象C,故③正确.
由于当x=
时,f(
)=3sin
=
≠0,故函数f(x)的图象C不关于点(
,0)对称,故④不正确,
故答案为:①②③.
| π |
| 3 |
| 11 |
| 12 |
| 3π |
| 2 |
| 11 |
| 12 |
令 2kπ-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 12 |
| 5π |
| 12 |
| π |
| 12 |
| 5π |
| 12 |
故f(x)在区间(-
| π |
| 12 |
| 5π |
| 12 |
将y=sin(2x-
| π |
| 3 |
| π |
| 3 |
由于当x=
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
3
| ||
| 2 |
| π |
| 3 |
故答案为:①②③.

练习册系列答案
相关题目
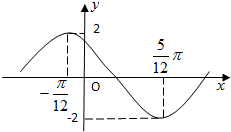

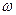 x+
x+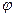 )(
)(