题目内容
1.已知实数x,y满足约束条件$\left\{\begin{array}{l}{x+y+5≥0}\\{x-y≤0}\\{y≤0}\end{array}\right.$,则z=2x+4y-3的最大值是-3.分析 利用z=2x+4y-3表示与y=-$\frac{1}{2}$x+$\frac{3}{4}$平行且与满足约束条件的实数x、y所构成的△OAB相交的直线,进而计算可得结论.
解答 解:依题意,满足约束条件的实数x、y所构成的图象为△OAB,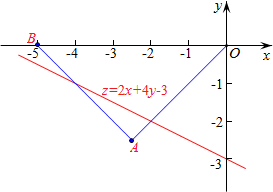
其A(-2.5,-2.5),B(-5,0),
令z=2x+4y-3=0,则y=-$\frac{1}{2}$x+$\frac{3}{4}$,
于是z=2x+4y-3表示与y=-$\frac{1}{2}$x+$\frac{3}{4}$平行且与△OAB相交的直线,
∴当其过原点时取最大值为-3,
故答案为:-3.
点评 本题考查简单线性规划,考查数列结合,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
12.平行六面体ABCD-A1B1C1D1中,AB=5,AD=3,AA1=7,∠CBA=120°,∠BAA1=∠DAA1=45°,则AC1的长等于( )
| A. | 83 | B. | $\sqrt{83}$ | C. | 98$+56\sqrt{2}$ | D. | $\sqrt{98+56\sqrt{2}}$ |
9.某空间几何体的三视图如图所示,则此几何体的体积为( )
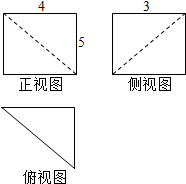

| A. | 10 | B. | 15 | C. | 20 | D. | 30 |
16.某班的课桌分4个大组摆放,每大组课桌数相同,甲、乙均为该班学生,则甲、乙两人的课桌在同一大组的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
11.若复数z满足(z+1)i=2-i,则复数z的共轭复数在复平面上所对应点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
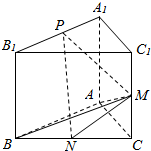 如图,已知三棱柱ABC-A1B1C1的侧面与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N、P分别是CC1、BC、A1B1的中点.
如图,已知三棱柱ABC-A1B1C1的侧面与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N、P分别是CC1、BC、A1B1的中点.