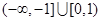题目内容
已知点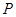 是双曲线
是双曲线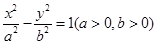 和圆
和圆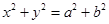 的一个交点,
的一个交点,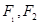 是双曲线的两个焦点,
是双曲线的两个焦点,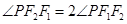 ,则双曲线的离心率为
,则双曲线的离心率为
 是双曲线
是双曲线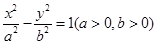 和圆
和圆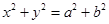 的一个交点,
的一个交点,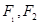 是双曲线的两个焦点,
是双曲线的两个焦点,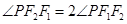 ,则双曲线的离心率为
,则双曲线的离心率为A.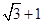 | B.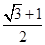 | C.2 | D.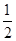 |
A
试题分析:∵双曲线方程为
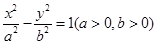 ,
,∴双曲线的焦点坐标为F1(-c,0)、F2(c,0),其中c=
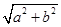 ,
,∵圆方程为x2+y2=a2+b2,即x2+y2=c2
∴该半径等于c,且圆经过F1和F2.
∵点P是双曲线
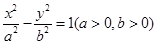 与圆x2+y2=a2+b2的交点,
与圆x2+y2=a2+b2的交点,∴△PF1F2中,|OP|=c=
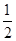 |F1F2|,可得∠F1PF2=90°,∵∠PF2F1=2∠PF1F2,且∠PF2F1+∠PF1F2=90°,
|F1F2|,可得∠F1PF2=90°,∵∠PF2F1=2∠PF1F2,且∠PF2F1+∠PF1F2=90°,∴∠PF1F2=30°,且∠PF2F1=60°,由此可得|PF1|=
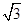 c,|PF2|=c,
c,|PF2|=c,根据双曲线定义,可得2a=|PF1|-|PF2|=(
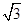 -1)c,
-1)c,∴双曲线的离心率e=
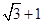 ,故选A。
,故选A。点评:中档题,在已知焦点三角形中的角度关系下求双曲线的离心率,往往需要探究三角形的特征,结合双曲线的定义,建立方程(组)加以解答。

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
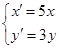 后,曲线C变为曲线
后,曲线C变为曲线 ,则曲线C的方程为 ( )
,则曲线C的方程为 ( ) 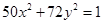
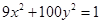
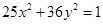
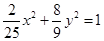
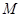 :
: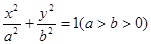 的离心率为
的离心率为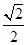 ,点
,点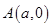 、
、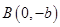 ,原点
,原点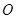 到直线
到直线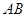 的距离为
的距离为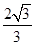 .
.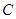
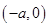 ,点
,点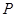 在椭圆
在椭圆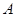 、
、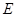 在直线
在直线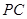 上,若直线
上,若直线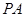 的方程为
的方程为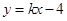 ,且
,且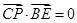 ,试求直线
,试求直线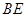 的方程.
的方程.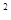 =2x于M(x
=2x于M(x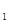 ,y
,y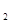 ,y
,y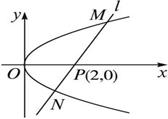
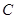 经过点
经过点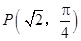 ,圆心为直线
,圆心为直线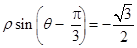 与极轴的交点,求圆
与极轴的交点,求圆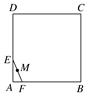
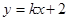 与双曲线
与双曲线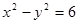 的右支交于不同的两点,那么
的右支交于不同的两点,那么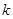 的取值范围是( )
的取值范围是( )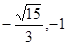 )
)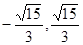 )
)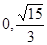 )
)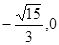 )
)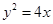 的焦点为圆心,且过坐标原点的圆的方程为( )
的焦点为圆心,且过坐标原点的圆的方程为( )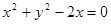
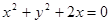
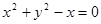
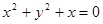
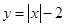 的图像与曲线
的图像与曲线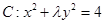 恰好有两个不同的公共点,则实数
恰好有两个不同的公共点,则实数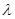 的取值范围是
的取值范围是