题目内容
如果函数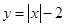 的图像与曲线
的图像与曲线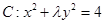 恰好有两个不同的公共点,则实数
恰好有两个不同的公共点,则实数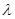 的取值范围是
的取值范围是
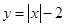 的图像与曲线
的图像与曲线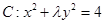 恰好有两个不同的公共点,则实数
恰好有两个不同的公共点,则实数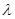 的取值范围是
的取值范围是A.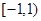 | B.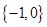 | C.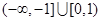 | D.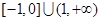 |
A
试题分析:解:由
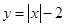 可得,x≥0时,y=x-2;x<0时,y=-x-2,∴函数
可得,x≥0时,y=x-2;x<0时,y=-x-2,∴函数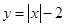 的图象与方程x2+λy2=1的曲线必相交于(±1,0)所以为了使函数
的图象与方程x2+λy2=1的曲线必相交于(±1,0)所以为了使函数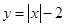 图象与方程x2+λy2=1的曲线恰好有两个不同的公共点,则y=x-1代入方程x2+λy2=1,整理可得(1+λ)x2-2λx+λ-1=0,当λ=-1时,x=1满足题意,由于△>0,1是方程的根,∴
图象与方程x2+λy2=1的曲线恰好有两个不同的公共点,则y=x-1代入方程x2+λy2=1,整理可得(1+λ)x2-2λx+λ-1=0,当λ=-1时,x=1满足题意,由于△>0,1是方程的根,∴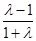 <0,即-1<λ<1时,方程两根异号,满足题意; y=-x-1代入方程x2+λy2=1,整理可得(1+λ)x2+2λx+λ-1=0,当λ=-1时,x=-1满足题意,由于△>0,-1是方程的根,∴
<0,即-1<λ<1时,方程两根异号,满足题意; y=-x-1代入方程x2+λy2=1,整理可得(1+λ)x2+2λx+λ-1=0,当λ=-1时,x=-1满足题意,由于△>0,-1是方程的根,∴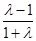 <0,即-1<λ<1时,方程两根异号,满足题意;,综上知,实数λ的取值范围是[-1,1),故选A
<0,即-1<λ<1时,方程两根异号,满足题意;,综上知,实数λ的取值范围是[-1,1),故选A点评:本题考查曲线的交点,考查学生分析解决问题的能力,考查分类讨论的数学思想,属于中档题

练习册系列答案
相关题目
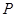 到点
到点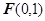 的距离与点
的距离与点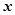 轴的距离的差等于1.(I)求动点
轴的距离的差等于1.(I)求动点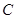 的方程;(II)过点
的方程;(II)过点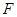 作两条斜率存在且互相垂直的直线
作两条斜率存在且互相垂直的直线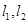 ,设
,设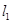 与轨迹
与轨迹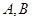 ,
,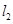 与轨迹
与轨迹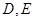 ,求
,求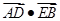 的最小值.
的最小值.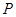 是双曲线
是双曲线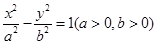 和圆
和圆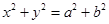 的一个交点,
的一个交点,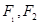 是双曲线的两个焦点,
是双曲线的两个焦点,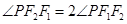 ,则双曲线的离心率为
,则双曲线的离心率为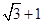
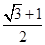
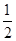
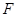 是椭圆
是椭圆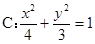 的右焦点,定点A
的右焦点,定点A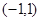 ,M是椭圆上的动点,则
,M是椭圆上的动点,则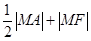 的最小值为 .
的最小值为 . 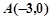 和圆
和圆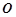 :
: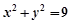 ,
,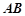 是圆
是圆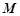 和
和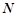 是
是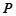 (异于
(异于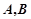 )是圆
)是圆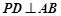 于
于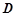 ,
,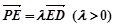 ,直线
,直线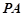 与
与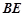 交于
交于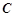 ,则当
,则当 时,
时,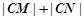 为定值.
为定值.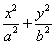 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为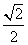 ,以该椭圆上的点和椭圆的左、右焦点F1、F2为顶点的三角形的周长为4(
,以该椭圆上的点和椭圆的左、右焦点F1、F2为顶点的三角形的周长为4(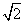 +1),一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D.
+1),一等轴双曲线的顶点是该椭圆的焦点,设P为该双曲线上异于顶点的任一点,直线PF1和PF2与椭圆的交点分别为A、B和C、D. 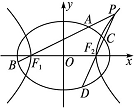
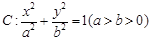 的长轴长是短轴长的两倍,焦距为
的长轴长是短轴长的两倍,焦距为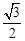 .
.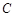 的标准方程;
的标准方程;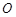 的直线
的直线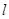 与椭圆
与椭圆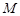 、
、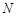 ,且直线
,且直线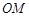 、
、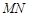 、
、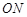 的斜率依次成等比数列,求△
的斜率依次成等比数列,求△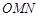 面积的取值范围.
面积的取值范围.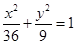 的弦被点
的弦被点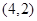 平分,则此弦所在的直线方程是 ( )
平分,则此弦所在的直线方程是 ( )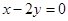
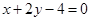
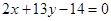
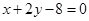
 过点
过点 与曲线
与曲线 恰有一个公共点,则满足条件的直线
恰有一个公共点,则满足条件的直线