题目内容
【题目】已知函数f(x)=![]() 的定义域为R.
的定义域为R.
(1)求a的取值范围;
(2)若函数f(x)的最小值为![]() ,解关于x的不等式x2-x-a2-a<0.
,解关于x的不等式x2-x-a2-a<0.
【答案】(1)[0,1];(2)![]() .
.
【解析】试题分析:
(1)原问题等价于ax2+2ax+1≥0恒成立,分类讨论:当a=0和a≠0两种情况可得a的取值范围是[0,1].
(2)由题意结合(1)的结论可得当x=-1时, f(x)min=![]() ,则
,则![]() =
=![]() ,a=
,a=![]() ,据此可得不等式x2-x-a2-a<0的解集为(-
,据此可得不等式x2-x-a2-a<0的解集为(-![]() ,
,![]() ).
).
试题解析:
(1)∵函数f(x)=![]() 的定义域为R,∴ax2+2ax+1≥0恒成立,分类讨论:
的定义域为R,∴ax2+2ax+1≥0恒成立,分类讨论:
当a=0时,1≥0恒成立.
当a≠0时,要满足题意,则有![]() ,解得0<a≤1.
,解得0<a≤1.
综上可知,a的取值范围是[0,1].
(2)f(x)=![]() =
=![]() ,由题意及(1)可知0<a≤1,
,由题意及(1)可知0<a≤1,
∴当x=-1时, f(x)min=![]() ,由题意得,
,由题意得,![]() =
=![]() ,∴a=
,∴a=![]() ,
,
∴不等式x2-x-a2-a<0可化为x2-x-![]() <0.解得-
<0.解得-![]() <x<
<x<![]() ,∴不等式的解集为(-
,∴不等式的解集为(-![]() ,
,![]() ).
).

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
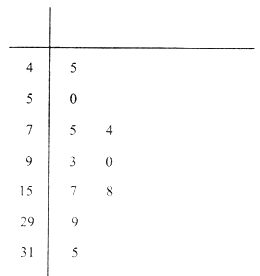
【题目】“共享单车”的出现,为我们提供了一种新型的交通方式.某机构为了调查人们对此种交通方式的满意度,从交通拥堵不严重的 ![]() 城市和交通拥堵严重的
城市和交通拥堵严重的 ![]() 城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图(如图所示):
城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图(如图所示):
若得分不低于80分,则认为该用户对此种交通方式“认可”,否则认为该用户对此种交通方式“不认可”,请根据此样本完成此 ![]() 列联表,并据此样本分析是否有
列联表,并据此样本分析是否有 ![]() 的把握认为城市拥堵与认可共享单车有关:
的把握认为城市拥堵与认可共享单车有关:
|
| 合计 | |
认可 | |||
不认可 | |||
合计 |
附:参考数据:(参考公式: ![]() )
)
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |