题目内容
(本小题满分14分)
如图,四棱锥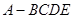 中,
中,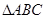 是正三角形,四边形
是正三角形,四边形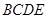 是矩形,且平面
是矩形,且平面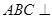 平面
平面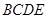 ,
, ,
, .
.

(Ⅰ) 若点 是
是 的中点,求证:
的中点,求证: 平面
平面 ;
;
(II)试问点 在线段
在线段 上什么位置时,二面角
上什么位置时,二面角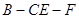 的余弦值为
的余弦值为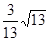 .
.
【答案】
.(Ⅰ)见解析;(Ⅱ)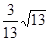 .
.
【解析】本试题主要是考查了立体几何中的二面角的求解,以及线面平行证明的综合运用。
(1)设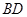 ,
, 交于点
交于点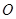 ,连接
,连接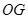 ,易知
,易知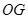 为
为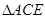 的中位线,故
的中位线,故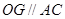 ,又
,又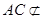 平面
平面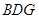 ,
, 平面
平面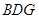 ,得
,得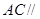 平面
平面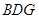
(2)合理的建立空间直角坐标系,然后求解平面的法向量,运用法向量与法向量的夹角来表示二面角的平面角的大小得到结论。
(Ⅰ)证明:设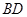 ,
, 交于点
交于点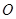 ,连接
,连接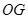 ,易知
,易知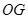 为
为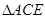 的中位线,故
的中位线,故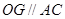 ,又
,又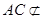 平面
平面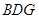 ,
, 平面
平面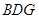 ,得
,得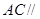 平面
平面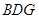 .………4分
.………4分
(Ⅱ)解:如图,建立空间直角坐标系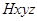 ,
,
在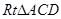 中,斜边
中,斜边 ,
,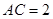 ,得
,得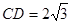 ∴
∴ ,
,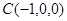 ,
,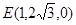 .设
.设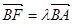 ,得
,得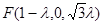 .
.
设平面 的一个法向量为
的一个法向量为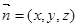 ,由
,由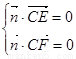 ,即
,即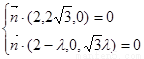 ,
,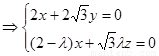 ,取
,取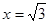 ,得
,得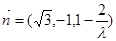 .
.
而平面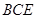 的法向量
的法向量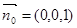 ,∴由题得
,∴由题得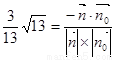 ,
,
即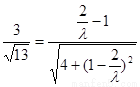 ,解得
,解得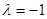 (舍去)或
(舍去)或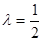 .
.
∴当点 在线段
在线段 的中点时,二面角
的中点时,二面角 的余弦值为
的余弦值为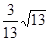 .…………14分
.…………14分

练习册系列答案
相关题目
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)