ΧβΡΩΡΎ»ί
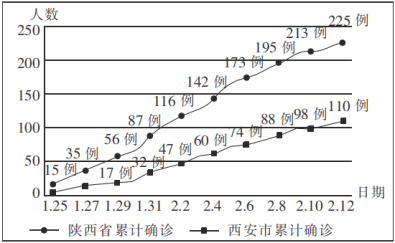
ΓΨΧβΡΩΓΩ‘ΎΆ≥ΦΤΒς≤ι÷–Θ§Έ ΨμΒΡ…ηΦΤ «“ΜΟ≈Κή¥σΒΡ―ßΈ Θ§ΧΊ±π «Ε‘“Μ–©ΟτΗ––‘Έ Χβ.άΐ»γ―ß…ζ‘ΎΩΦ ‘÷–”–ΈόΉς±Ήœ÷œσΘ§…γΜα…œΒΡΆΒΥΑ¬©ΥΑΒ».Ηϋ“ΣΨΪ–Ρ…ηΦΤΈ Ψμ.…ηΖ®œϊ≥ΐ±ΜΒς≤ι’ΏΒΡΙΥ¬«Θ§ ΙΥϊΟ«ΡήΙΜ»γ ΒΜΊ¥πΈ ΧβΘ§Ζώ‘ρ±ΜΒς≤ι’ΏΆυΆυΜαΨήΨχÉ’¥πΘ§Μρ≤ΜΧαΙ©’φ Β«ιΩωΘ§ΈΣΝΥΒς≤ι÷–―ß…ζ÷–ΒΡ‘γΝΒœ÷œσΘ§ΥφΜζ≥ι≥ω300Οϊ―ß…ζΘ§Βς≤ι÷– Ι”ΟΝΥΝΫΗωΈ ν}.ΔΌΡψΒΡ―ßΦ°Κ≈ΒΡΉνΚσ“ΜΈΜ ΐ «Τφ ΐΘ®―ßΦ°Κ≈ΒΡΚσΥΡΈΜ «–ρΚ≈Θ©ΘΜΔΎΡψ «Ζώ”–‘γΝΒœ÷œσΘ§»Ο±ΜΒς≤ι’Ώ¥”ΉΑ”–4ΗωΚλ«ρΘ§6ΗωΚΎ«ρΘ®≥ΐ―’…ΪΆβΆξ»ΪœύΆ§Θ©ΒΡ¥ϋΉ”÷–ΥφΜζΟΰ»ΓΝΫΗω«ρ.ΟΰΒΫΝΫ«ρΆ§…ΪΒΡ―ß…ζ»γ ΒΜΊ¥πΒΎ“ΜΗωΈ ΧβΘ§ΟΰΒΫΝΫ«ρ“λ…ΪΒΡ―ß…ζ»γ ΒΜΊ¥πΒΎΕΰΗωΈ ΧβΘ§ΜΊ¥πΓΑ «Γ±ΒΡ»ΥΆυ“ΜΗωΚ–Ή”÷–Ζ≈“ΜΗω–Γ ·Ή”Θ§ΜΊ¥πΓΑΖώΓ±ΒΡ»Υ ≤Ο¥ΕΦ≤ΜΖ≈Θ§Κσά¥‘ΎΚ–Ή”÷– ’ΒΫΝΥ78Ηω–Γ ·Ή”.
Θ®1Θ©ΡψΡήΖώΙάΥψ≥ω÷–―ß…ζ‘γΝΒ»Υ ΐΒΡΑΌΖ÷±»ΘΩ
Θ®2Θ©»τ¥”ΗΟΒΊ«χ÷–―ß…ζ÷–ΥφΜζ≥ι»Γ“ΜΗωΑύΘ®40»ΥΘ©Θ§…ηΤδ÷–«Γ”–![]() Ηω»Υ¥φ‘Ύ‘γΝΒΒΡœ÷œσΘ§«σ
Ηω»Υ¥φ‘Ύ‘γΝΒΒΡœ÷œσΘ§«σ![]() ΒΡΖ÷≤ΦΝ–ΦΑ ΐ―ßΤΎΆϊ.
ΒΡΖ÷≤ΦΝ–ΦΑ ΐ―ßΤΎΆϊ.
ΓΨ¥πΑΗΓΩ(1)![]() ΘΜ(2)Ζ÷≤ΦΝ–ΦϊœξΫβΘ§ ΐ―ßΤΎΆϊΈΣ
ΘΜ(2)Ζ÷≤ΦΝ–ΦϊœξΫβΘ§ ΐ―ßΤΎΆϊΈΣ![]() .
.
ΓΨΫβΈωΓΩ
Θ®1Θ©œ»ΦΤΥψ≥ωΟΰΝΫΗω«ρΘ§≥ωœ÷Ά§…ΪΚΆ“λ…ΪΒΡΗ≈¬ Θ§Ψί¥ΥΦΤΥψ≥ωΜΊ¥πΒΎ“ΜΗωΈ ΧβΚΆΒΎΕΰΗωΈ ΧβΒΡ»Υ ΐΘ§‘ΌΗυΨί―ßΦ°Κ≈ΉνΚσ“ΜΈΜ «Τφ ΐΒΡΗ≈¬ ΈΣ![]() Θ§ΦΤΥψ≥ωΜΊ¥πΒΎ“ΜΗωΈ Χβ―Γ‘ώΓΑ «Γ±ΒΡΆ§―ßΗω ΐΘ§¥”ΕχΥψ≥ωΜΊ¥π‘γΝΒ―Γ‘ώΓΑ «Γ±ΒΡΆ§―ßΗω ΐΘ§Ψί¥ΥΙάΥψΑΌΖ÷±»Φ¥Ω…ΘΜ
Θ§ΦΤΥψ≥ωΜΊ¥πΒΎ“ΜΗωΈ Χβ―Γ‘ώΓΑ «Γ±ΒΡΆ§―ßΗω ΐΘ§¥”ΕχΥψ≥ωΜΊ¥π‘γΝΒ―Γ‘ώΓΑ «Γ±ΒΡΆ§―ßΗω ΐΘ§Ψί¥ΥΙάΥψΑΌΖ÷±»Φ¥Ω…ΘΜ
Θ®2Θ©ΗυΨίΧβ“βΩ…÷ΣΘ§![]() Ζΰ¥”ΕΰœνΖ÷≤ΦΘ§ΫαΚœΘ®1Θ©÷–Υυ«σΘ§–¥≥ωΖ÷≤ΦΝ–Θ§ΦΤΥψ≥ω ΐ―ßΤΎΆϊΦ¥Ω….
Ζΰ¥”ΕΰœνΖ÷≤ΦΘ§ΫαΚœΘ®1Θ©÷–Υυ«σΘ§–¥≥ωΖ÷≤ΦΝ–Θ§ΦΤΥψ≥ω ΐ―ßΤΎΆϊΦ¥Ω….
Θ®1Θ©¥”10Ηω«ρ÷–ΥφΜζΟΰ»ΓΝΫΗω«ρΘ§ΟΰΒΫΝΫ«ρΆ§…ΪΒΡΒΡΗ≈¬ ![]() .
.
Ι ΜΊ¥πΒΎ“ΜΗωΈ ΧβΒΡ»Υ ΐΈΣ![]() »ΥΘ§‘ρΜΊ¥πΒΎΕΰΗωΈ ΧβΒΡ»Υ ΐΈΣ
»ΥΘ§‘ρΜΊ¥πΒΎΕΰΗωΈ ΧβΒΡ»Υ ΐΈΣ![]() »ΥΘΜ
»ΥΘΜ
”÷―ßΦ°Κ≈ΉνΚσ“ΜΈΜ «Τφ ΐΜΙ «≈Φ ΐΘ§ «Β»Ω…ΡήΒΡΘ§
Ι ΜΊ¥πΒΎ“ΜΗωΈ ΧβΘ§―Γ‘ώΓΑ «Γ± «ΒΡΆ§―ßΗω ΐΈΣ![]() »ΥΘ§
»ΥΘ§
‘ρΜΊ¥πΒΎΕΰΗωΈ ΧβΘ§―Γ‘ώΓΑ «Γ±ΒΡΆ§―ßΗω ΐΈΣ![]() »ΥΘ§
»ΥΘ§
‘ρ÷–―ß…ζ‘γΝΒ»Υ ΐΒΡΑΌΖ÷±»ΈΣ![]() .
.
Θ®2Θ©ΗυΨίΘ®1Θ©÷–Υυ«σΘ§Ω…÷Σ![]() Θ§«“
Θ§«“![]() Ω…»Γ÷ΒΈΣ
Ω…»Γ÷ΒΈΣ![]() Θ§
Θ§
Ι Ω…ΒΟ![]()
![]()
![]()
Ι ![]() ΒΡΖ÷≤ΦΝ–»γœ¬Υυ ΨΘΚ
ΒΡΖ÷≤ΦΝ–»γœ¬Υυ ΨΘΚ
|
|
|
|
|
|
|
|
Ι ![]() .
.

ΓΨΧβΡΩΓΩΡ≥ΙΪΥΨΈΣΝΥΕ‘Ρ≥÷÷…ΧΤΖΫχ––ΚœάμΕ®ΦέΘ§–ηΝΥΫβΗΟ…ΧΤΖΒΡ‘¬œζ έΝΩ![]() Θ®ΒΞΈΜΘΚΆρΦΰΘ©”ꑬœζ έΒΞΦέ
Θ®ΒΞΈΜΘΚΆρΦΰΘ©”ꑬœζ έΒΞΦέ![]() Θ®ΒΞΈΜΘΚ‘Σ/ΦΰΘ©÷°ΦδΒΡΙΊœΒΘ§Ε‘Ϋϋ
Θ®ΒΞΈΜΘΚ‘Σ/ΦΰΘ©÷°ΦδΒΡΙΊœΒΘ§Ε‘Ϋϋ![]() Ηω‘¬ΒΡ‘¬œζ έΝΩ
Ηω‘¬ΒΡ‘¬œζ έΝΩ![]() ΚΆ‘¬œζ έΒΞΦέ
ΚΆ‘¬œζ έΒΞΦέ![]()
![]() ΐΨίΫχ––ΝΥΆ≥ΦΤΖ÷ΈωΘ§ΒΟΒΫ“ΜΉιΦλ≤β ΐΨί»γ±μΥυ ΨΘΚ
ΐΨίΫχ––ΝΥΆ≥ΦΤΖ÷ΈωΘ§ΒΟΒΫ“ΜΉιΦλ≤β ΐΨί»γ±μΥυ ΨΘΚ
‘¬œζ έΒΞΦέ |
|
|
|
|
|
|
‘¬œζ έΝΩ |
|
|
|
|
|
|
Θ®1Θ©»τ”ΟœΏ–‘ΜΊΙιΡΘ–ΆΡβΚœ![]() ”κ
”κ![]() ÷°ΦδΒΡΙΊœΒΘ§œ÷”–ΦΉΓΔ““ΓΔ±ϊ»ΐΈΜ ΒœΑ‘±ΙΛ«σΒΟΜΊΙι÷±œΏΖΫ≥ΧΖ÷±πΈΣΘΚ
÷°ΦδΒΡΙΊœΒΘ§œ÷”–ΦΉΓΔ““ΓΔ±ϊ»ΐΈΜ ΒœΑ‘±ΙΛ«σΒΟΜΊΙι÷±œΏΖΫ≥ΧΖ÷±πΈΣΘΚ![]() Θ§
Θ§![]() ΚΆ
ΚΆ![]() Θ§Τδ÷–”–«“Ϋω”–“ΜΈΜ ΒœΑ‘±ΙΛΒΡΦΤΥψΫαΙϊ «’ΐ»ΖΒΡΘ°«κΫαΚœΆ≥ΦΤ―ßΒΡœύΙΊ÷Σ ΕΘ§≈–ΕœΡΡΈΜ ΒœΑ‘±ΙΛΒΡΦΤΥψΫαΙϊ «’ΐ»ΖΒΡΘ§≤ΔΥΒΟςάμ”…ΘΜ
Θ§Τδ÷–”–«“Ϋω”–“ΜΈΜ ΒœΑ‘±ΙΛΒΡΦΤΥψΫαΙϊ «’ΐ»ΖΒΡΘ°«κΫαΚœΆ≥ΦΤ―ßΒΡœύΙΊ÷Σ ΕΘ§≈–ΕœΡΡΈΜ ΒœΑ‘±ΙΛΒΡΦΤΥψΫαΙϊ «’ΐ»ΖΒΡΘ§≤ΔΥΒΟςάμ”…ΘΜ
Θ®2Θ©»τ”Ο![]() ΡΘ–ΆΡβΚœ
ΡΘ–ΆΡβΚœ![]() ”κ
”κ![]() ÷°ΦδΒΡΙΊœΒΘ§Ω…ΒΟΜΊΙιΖΫ≥ΧΈΣ
÷°ΦδΒΡΙΊœΒΘ§Ω…ΒΟΜΊΙιΖΫ≥ΧΈΣ![]() Θ§Ψ≠ΦΤΥψΗΟΡΘ–ΆΚΆΘ®1Θ©÷–’ΐ»ΖΒΡœΏ–‘ΜΊΙιΡΘ–ΆΒΡœύΙΊ÷Η ΐ
Θ§Ψ≠ΦΤΥψΗΟΡΘ–ΆΚΆΘ®1Θ©÷–’ΐ»ΖΒΡœΏ–‘ΜΊΙιΡΘ–ΆΒΡœύΙΊ÷Η ΐ![]() Ζ÷±πΈΣ
Ζ÷±πΈΣ![]() ΚΆ
ΚΆ![]() Θ§«κ”Ο
Θ§«κ”Ο![]() ΥΒΟςΡΡΗωΜΊΙιΡΘ–ΆΒΡΡβΚœ–ßΙϊΗϋΚΟΘΜ
ΥΒΟςΡΡΗωΜΊΙιΡΘ–ΆΒΡΡβΚœ–ßΙϊΗϋΚΟΘΜ
Θ®3Θ©“―÷ΣΗΟ…ΧΤΖΒΡ‘¬œζ έΕνΈΣ![]() Θ®ΒΞΈΜΘΚΆρ‘ΣΘ©Θ§άϊ”ΟΘ®2Θ©÷–ΒΡΫαΙϊΜΊ¥πΈ ΧβΘΚΒ±‘¬œζ έΒΞΦέΈΣΚΈ÷Β ±Θ§…ΧΤΖΒΡ‘¬œζ έΕν‘Λ±®÷ΒΉν¥σΘΩΘ®ΨΪ»ΖΒΫ
Θ®ΒΞΈΜΘΚΆρ‘ΣΘ©Θ§άϊ”ΟΘ®2Θ©÷–ΒΡΫαΙϊΜΊ¥πΈ ΧβΘΚΒ±‘¬œζ έΒΞΦέΈΣΚΈ÷Β ±Θ§…ΧΤΖΒΡ‘¬œζ έΕν‘Λ±®÷ΒΉν¥σΘΩΘ®ΨΪ»ΖΒΫ![]() Θ©
Θ©
≤ΈΩΦ ΐΨίΘΚ![]() .
.