题目内容
8.已知m∈R,n∈R,并且m+3n=1,则mem+3ne3n的最小值$\sqrt{e}$.分析 先根据等式将n消去,构造函数f(m)=m•em+3n•e3n=m•em+(1-m)•e1-m 然后讨论m,研究函数的单调性求出最小值即可.
解答 解:∵3n=1-m,
∴f(m)=m•em+3n•e3n=m•em+(1-m)•e1-m
令g(m)=m•em,h(m)=(1-m)•e1-m
当m≤0时,h(m)为减函数,且h(m)≥h(0)=e,
g(m)=-|m|•e-|m|由于从y=x与y=ex的图象易知,|m|≤e|m|,
所以|m|•e-|m|≤$\frac{1}{e}$,
g(m)=-|m|•e-|m|≥-$\frac{1}{e}$,
f(m)=g(m)+h(m)≥-$\frac{1}{e}$+e,
当m≥$\frac{1}{2}$时,由g(m)与h(m)关于x=$\frac{1}{2}$对称,同上可得f(m)≥e-$\frac{1}{e}$,
当 0<m<$\frac{1}{2}$时,g(0)=h(1)=0,g(1)=h(0)=e,
g′(m)=(m+1)em>0,h′(m)=-(2-m)e1-m<0
且g′(m),h′(m)均为单调递增,
当0<m<$\frac{1}{2}$时,g′(m)<g′($\frac{1}{2}$)=$\frac{3}{2}$$\sqrt{e}$,h′(m)<h′($\frac{1}{2}$)=-$\frac{3}{2}$$\sqrt{e}$,
f′(m)=g′(m)+h′(m)<0单调递减,
当$\frac{1}{2}$≤m<1时,同理,可得f′(m)=g′(m)+h′(m)≥g′($\frac{1}{2}$)+h′($\frac{1}{2}$)=0单调递增
(当m=$\frac{1}{2}$时等号成立)
所以当m=$\frac{1}{2}$时,f(m)取最小值,
即当m=$\frac{1}{2}$,n=$\frac{1}{6}$时,mem+3ne3n的最小值为$\sqrt{e}$.
故答案为:$\sqrt{e}$.
点评 本题主要考查了利用导数研究函数的单调性,同时考查了分类讨论的数学思想和转化的思想,属于难题.

 阅读快车系列答案
阅读快车系列答案| A. | ab>0 | B. | ab>1 | C. | ab≤0 | D. | ab≤1 |
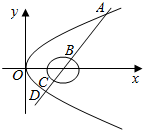 如图,直线y=x-2与圆x2+y2-4x+3=0及抛物线y2=8x依次交于A、B、C、D四点,则|AB|+|CD|=14.
如图,直线y=x-2与圆x2+y2-4x+3=0及抛物线y2=8x依次交于A、B、C、D四点,则|AB|+|CD|=14.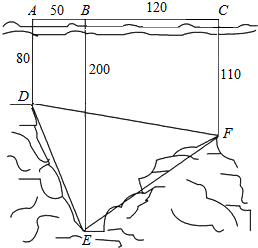 马航MH370牵动全球人的心,世界各国积极投身到马航的搜救工作中,了解海底构造是救援工作要做的第一件事.某搜救队在某海域的海平面上的同一条直线上的A,B,C三点进行测量,得AB=50,BC=120,于A,B,C三处测得水深分别为AD=80,BE=200,CF=110,如图所示,试利用你所学知识求∠DEF的余弦值.
马航MH370牵动全球人的心,世界各国积极投身到马航的搜救工作中,了解海底构造是救援工作要做的第一件事.某搜救队在某海域的海平面上的同一条直线上的A,B,C三点进行测量,得AB=50,BC=120,于A,B,C三处测得水深分别为AD=80,BE=200,CF=110,如图所示,试利用你所学知识求∠DEF的余弦值.