某三棱锥的三视图如图所示.则该三棱锥的体积是( )A．4B．$\frac{8}{3}$C．2D．$\frac{4}{3}$ 题目和参考答案——青夏教育精英家教网——

题目内容

19．某三棱锥的三视图如图所示，则该三棱锥的体积是（　　）

A．

4

B．

$\frac{8}{3}$

C．

2

D．

$\frac{4}{3}$

分析根据几何体的三视图，得出该几何体是高为2的三棱锥，结合图中数据，求出它的体积．

解答解：根据几何体的三视图，得；
该几何体是一底面为三角形，高为2的三棱锥，
且底面三角形的底边长为4，底边上的高为2，
如图所示；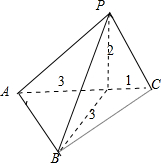
∴该三棱锥的体积是
V_几何体=$\frac{1}{3}$S_△ABC•h=$\frac{1}{3}×$$\frac{1}{2}$×4×3×2=4．
故选：A．

点评本题考查了利用空间几何体的三视图求几何体的体积的应用问题，是基础题目．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

11．若$f（x）=\left\{{\begin{array}{l}{{3^x}，x∈[-1，0）}\\{-{{（\frac{1}{3}）}^x}，x∈[0，1]}\end{array}}\right.$，则f[f（log₃2）]的值为$\frac{\sqrt{3}}{3}$．

10．已知a∈R，f（x）=（x²-4）（x-a）．
（1）求f′（x）；
（2）若f′（-1）=0，求f（x）在[-2，2]上的最大值和最小值；
（3）若f（x）在（-∞，-2]和[2，+∞）上是单调递增的，求实数a的取值范围．

7．已知△ABC的三个顶点在以O为球心的球面上，a，b，c分别为△ABC的三个内角A，B，C的对边，满足$a=\sqrt{3}，b=1$，且（a+b）（sinA-sinB）=（c+b）sinC，若三棱锥O-ABC的体积为$\frac{{\sqrt{5}}}{4}$，则球O的表面积为64π．

14．求下列函数的最小正周期及对称中心．
（1）f（x）=$\sqrt{co{s}^{2}x-co{s}^{4}x}$；
（2）f（x）=cos$\frac{π}{2}$x•cos[$\frac{π}{2}$（x-1）]；
（3）f（x）=sinx•cosx-2sin³xcosx；
（4）f（x）=sin⁶x+cos⁶x．

4．已知集合A={x∈R|$\frac{x-2}{x}$＞0}，B={x∈R|y=ln（x-1）}，则∁_UA∩B=（　　）

11．在△ABC中，∠A=45°，∠C=105°，BC=$\sqrt{2}$则AC为（　　）

8．求不等式$|{\sqrt{3x-2}-3}|＞1$．

9．已知等比数列{a_n}的首项a₁、公比q是关于x的方程（t-1）x²+2x+（2t-1）=0的实数解，若数列{a_n}有且只有一个，则实数t的取值集合为$\{0，\frac{1}{2}，1，\frac{3}{2}\}$．