题目内容
【题目】已知椭圆 ![]() 的焦点和上顶点分别为F1、F2、B,定义:△F1BF2为椭圆C的“特征三角形”,如果两个椭圆的特征三角形是相似三角形,那么称这两个椭圆为“相似椭圆”,且特征三角形的相似比即为相似椭圆的相似比,已知点
的焦点和上顶点分别为F1、F2、B,定义:△F1BF2为椭圆C的“特征三角形”,如果两个椭圆的特征三角形是相似三角形,那么称这两个椭圆为“相似椭圆”,且特征三角形的相似比即为相似椭圆的相似比,已知点 ![]() 是椭圆
是椭圆 ![]() 的一个焦点,且C1上任意一点到它的两焦点的距离之和为4.
的一个焦点,且C1上任意一点到它的两焦点的距离之和为4.
(1)若椭圆C2与椭圆C1相似,且C2与C1的相似比为2:1,求椭圆C2的方程;
(2)已知点P(m,n)(mn≠0)是椭圆C1上的任意一点,若点Q是直线y=nx与抛物线 ![]() 异于原点的交点,证明:点Q一定在双曲线4x2﹣4y2=1上;
异于原点的交点,证明:点Q一定在双曲线4x2﹣4y2=1上;
(3)已知直线l:y=x+1,与椭圆C1相似且短半轴长为b的椭圆为Cb , 是否存在正方形ABCD,(设其面积为S),使得A、C在直线l上,B、D在曲线Cb上?若存在,求出函数S=f(b)的解析式及定义域;若不存在,请说明理由.
【答案】
(1)解:椭圆的一个焦点为 ![]() ,|PF1|+|PF2|=2a=4,
,|PF1|+|PF2|=2a=4,
∴b2=a2﹣c2=1,则椭圆C1: ![]() ,
,
设C2: ![]() ,相似比为2,a2=4;b2=2,
,相似比为2,a2=4;b2=2,
∴椭圆C2: ![]()
(2)证明:点P(m,n)在椭圆上,则 ![]() ,设点Q(x0,y0),
,设点Q(x0,y0),
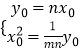 ,
, 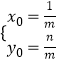 ,
,
∴4x02﹣4y02= ![]() ﹣
﹣ ![]() =
= ![]() =
= ![]() =1,
=1,
∴点Q在双曲线4x2﹣4y2=1上
(3)解:椭圆C1: ![]() ,相似比为b,则椭圆Cb的方程为:
,相似比为b,则椭圆Cb的方程为: ![]() ,
,
由题意:只需Cb上存在两点B、D关于直线y=x+1对称即可
设BD:y=﹣x+m,设BD中点为E(x0,y0),B(x1,y1),D(x2,y2),
![]() ,5x2﹣8mx+4m2﹣4b2=0,
,5x2﹣8mx+4m2﹣4b2=0,
△=64m2﹣16×5×(m2﹣b2)>0,5b2>m2,
由韦达定理知:x0= ![]() ,y0=﹣x0+m=
,y0=﹣x0+m= ![]() m,
m,
E(x0,y0)在直线y=x+1上,
则 ![]() m=
m= ![]() +1
+1
解得:m=﹣ ![]() ,∴b2>
,∴b2> ![]() ,则b>
,则b> ![]() ,
,
此时正方形的边长为 ![]() ,
,
∴正方形的面积为S=f(b)=( ![]() )2,
)2,
丨BD丨= ![]() =
= ![]() ,
,
∴函数S=f(b)的解析式: ![]() ,定义域为
,定义域为 ![]()
【解析】(1)由题意c= ![]() ,a=2,则b2=a2﹣c2=1,即可求得椭圆C1的方程,根据相似比2,a2=4;b2=2,即可求得椭圆C2的方程;(2)由题设条件知
,a=2,则b2=a2﹣c2=1,即可求得椭圆C1的方程,根据相似比2,a2=4;b2=2,即可求得椭圆C2的方程;(2)由题设条件知 ![]() ,设点Q(x0,y0),由题设条件能推出
,设点Q(x0,y0),由题设条件能推出 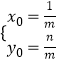 ,即可求得
,即可求得 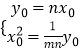 ,即可求得4x2﹣4y2=1;(3)椭圆C1:
,即可求得4x2﹣4y2=1;(3)椭圆C1: ![]() ,相似比为b,则椭圆Cb的方程,由题意:只需Cb上存在两点B、D关于直线y=x+1对称即可.设BD:y=﹣x+m,代入椭圆方程,设BD中点为E(x0,y0),然后利用根与系数的关系进行求解.
,相似比为b,则椭圆Cb的方程,由题意:只需Cb上存在两点B、D关于直线y=x+1对称即可.设BD:y=﹣x+m,代入椭圆方程,设BD中点为E(x0,y0),然后利用根与系数的关系进行求解.



