题目内容
已知函数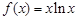 .
.
(Ⅰ)求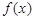 的最小值;
的最小值;
(Ⅱ)若对所有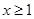 都有
都有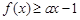 ,求实数
,求实数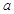 的取值范围.
的取值范围.
【答案】
(1)当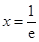 时,
时,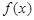 取得最小值
取得最小值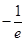 .
(2)
.
(2)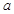 的取值范围是
的取值范围是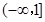 .
.
【解析】
试题分析:(1)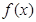 的定义域为
的定义域为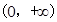 , 1分
, 1分
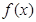 的导数
的导数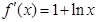 .
2分
.
2分
令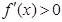 ,解得
,解得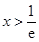 ;令
;令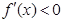 ,解得
,解得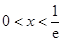 .
.
从而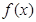 在
在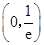 单调递减,在
单调递减,在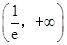 单调递增. 4分
单调递增. 4分
所以,当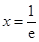 时,
时,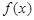 取得最小值
取得最小值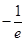 .
6分
.
6分
(2)依题意,得 在
在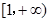 上恒成立,
上恒成立,
即不等式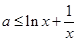 对于
对于 恒成立 .
恒成立 .
令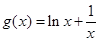 , 则
, 则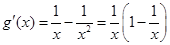 .
8分
.
8分
当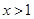 时,因为
时,因为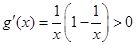 ,
,
故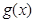 是
是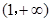 上的增函数, 所以
上的增函数, 所以
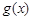 的最小值是
的最小值是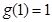 , 10分
, 10分
所以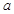 的取值范围是
的取值范围是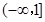 .
12分
.
12分
考点:应用导数研究函数的单调性、最值,不等式恒成立问题。
点评:中档题,本题属于导数应用中的常见问题,通过研究函数的单调性,明确最值情况。涉及不等式恒成立问题,往往通过构造函数,研究函数的最值,得到确定参数(范围)的目的。对数函数要注意其真数大于0.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(
| ||||
B、f(x)=2sin(
| ||||
C、f(x)=2sin(2x-
| ||||
D、f(x)=2sin(2x+
|