题目内容
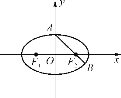
【题目】已知![]() 、
、![]() 是椭圆
是椭圆![]() (
(![]() )的左、右焦点,过
)的左、右焦点,过![]() 作
作![]() 轴的垂线与
轴的垂线与![]() 交于
交于![]() 、
、![]()
两点, ![]() 与
与![]() 轴交于点
轴交于点![]() ,
, ![]() ,且
,且![]() ,
, ![]() 为坐标原点.
为坐标原点.
(1)求![]() 的方程;
的方程;
(2)设![]() 为椭圆
为椭圆![]() 上任一异于顶点的点,
上任一异于顶点的点, ![]() 、
、![]() 为
为![]() 的上、下顶点,直线
的上、下顶点,直线![]() 、
、![]() 分别交
分别交![]() 轴于点
轴于点![]() 、
、![]() .若直线
.若直线![]() 与过点
与过点![]() 、
、![]() 的圆切于点
的圆切于点![]() .试问:
.试问: ![]() 是否为定值?若是,求出该定值;若不是,请说明理由。
是否为定值?若是,求出该定值;若不是,请说明理由。
【答案】(1)![]() .(2)见解析.
.(2)见解析.
【解析】试题分析:(1)由题可得![]() 为正三角形,由此求得
为正三角形,由此求得![]() ,又
,又![]() ,可求得
,可求得![]() ,
, ![]() .,得到椭圆的方程;
.,得到椭圆的方程;
2)由(1)可知, ![]() ,
, ![]()
设点![]() ,表示出
,表示出![]() 的坐标,设圆
的坐标,设圆![]() 的圆心为
的圆心为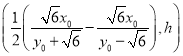 ,设圆
,设圆![]() 的半径为
的半径为![]() ,通过点在圆上,推出
,通过点在圆上,推出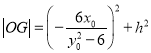 .然后求出
.然后求出![]() 的表达式,利用
的表达式,利用![]() ,化简即可求出
,化简即可求出![]() 的值
的值
试题解析:(1)由![]() 知点
知点![]() 是线段
是线段![]() 的中点,又
的中点,又![]() 为等腰三角形
为等腰三角形
且![]() ,得
,得![]() 为正三角形,
为正三角形,
![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() .
.
∵![]() ,且
,且![]()
∴![]() ,
, ![]() .
.
椭圆![]() 的方程为
的方程为![]() .
.
(2)设![]() ,由(1)知
,由(1)知![]() ,
, ![]() ,
, ![]()
则直线![]() 的方程为
的方程为![]() .
.
直线![]() 的方程为
的方程为![]() ,
,
∴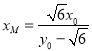 ,
, 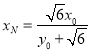 ,
,
设过![]() 的圆
的圆![]() 的圆心为
的圆心为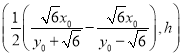
即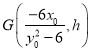 ,则
,则![]() 的半径
的半径![]() 满足;
满足;
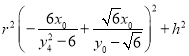
又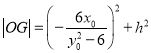
∴
![]()
∴![]() ,即
,即![]() 为定长.
为定长.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目