题目内容
【题目】如图,已知椭圆![]() =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上顶点,直线AF2交椭圆于另一点B.
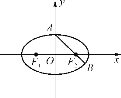
(1)若∠F1AB=90°,求椭圆的离心率;
(2)若![]() =2
=2![]() ,
,![]() ·
·![]() =
=![]() ,求椭圆的方程.
,求椭圆的方程.
【答案】(1)![]() (2)
(2)![]() =1
=1
【解析】(1)若∠F1AB=90°,则△AOF2为等腰直角三角形,所以有OA=OF2,即b=c.所以a=![]() c,e=
c,e=![]() =
=![]() .
.
(2)由题知A(0,b),F1(-c,0),F2(c,0),
其中,c=![]() ,设B(x,y).
,设B(x,y).
由![]() =2
=2![]() ,得(c,-b)=2(x-c,y),
,得(c,-b)=2(x-c,y),
解得x=![]() ,y=-
,y=-![]() ,即B
,即B![]() .
.
将B点坐标代入![]() =1,得
=1,得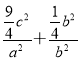 =1,即
=1,即![]() =1,解得a2=3c2.①
=1,解得a2=3c2.①
又由![]() ·
·![]() =(-c,-b)·
=(-c,-b)·![]() ,得b2-c2=1,即有a2-2c2=1.②
,得b2-c2=1,即有a2-2c2=1.②
由①②解得c2=1,a2=3,从而有b2=2.
所以椭圆方程为![]() =1.
=1.

练习册系列答案
相关题目

