题目内容
已知P、Q、M、N四点都在中心为坐标原点,离心率为
,左焦点为F(-1,0)的椭圆C上,已知
与
共线,
与
共线,
•
=0.
(1)求椭圆C的方程;
(2)试用直线PQ的斜率k(k≠0)表示四边形PMQN的面积S,求S的最小值.
| ||
| 2 |
| PF |
| FQ |
| MF |
| FN |
| PF |
| MF |
(1)求椭圆C的方程;
(2)试用直线PQ的斜率k(k≠0)表示四边形PMQN的面积S,求S的最小值.
分析:(1)设出椭圆方程,利用离心率为
,左焦点为F(-1,0)的椭圆C上,求出几何量,即可得到椭圆的方程;
(2)设出直线方程,代入椭圆方程,求出|PQ|,|MN|,表示出面积,利用基本不等式,即可得到结论.
| ||
| 2 |
(2)设出直线方程,代入椭圆方程,求出|PQ|,|MN|,表示出面积,利用基本不等式,即可得到结论.
解答:解:(1)设椭圆方程为
+
=1(a>b>0),则a2=b2+c2
∵c=1,
=
∴a=
,b=1
∴椭圆的方程为
+y2=1;
(2)由题意,PQ与MN垂直于F,设PQ的方程为y=k(x+1),与椭圆方程联立,可得
(1+2k2)x2+4k2x+2k2-2=0
设点P(x1,y1),Q(x2,y2),则x1+x2=-
,x1x2=
∴|PQ|=
|x1-x2|=
同理,|MN|=
∴SPMQN=
|PQ||MN|=2-
=2-
≥
当且仅当k=±1时,取等号
∴四边形PMQN的面积的最小值为
.
| x2 |
| a2 |
| y2 |
| b2 |
∵c=1,
| c |
| a |
| ||
| 2 |
∴a=
| 2 |
∴椭圆的方程为
| x2 |
| 2 |
(2)由题意,PQ与MN垂直于F,设PQ的方程为y=k(x+1),与椭圆方程联立,可得
(1+2k2)x2+4k2x+2k2-2=0
设点P(x1,y1),Q(x2,y2),则x1+x2=-
| 4k2 |
| 1+2k2 |
| 2k2-2 |
| 1+2k2 |
∴|PQ|=
| 1+k2 |
2
| ||
| 1+2k2 |
同理,|MN|=
2
| ||
| 2+k2 |
∴SPMQN=
| 1 |
| 2 |
| 2k2 |
| 2k4+5k2+2 |
| 2 | ||
2k2+
|
| 16 |
| 9 |
当且仅当k=±1时,取等号
∴四边形PMQN的面积的最小值为
| 16 |
| 9 |
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查四边形面积的计算,考查基本不等式的运用,属于中档题.

练习册系列答案
相关题目
 (2012•江苏二模)如图,已知椭圆C:
(2012•江苏二模)如图,已知椭圆C: ”的充分不必要条件
”的充分不必要条件 :对任意实数x,都有x2-x+1>0,则命题“p∧¬q”是真命题
:对任意实数x,都有x2-x+1>0,则命题“p∧¬q”是真命题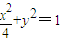 ,A、B是四条直线x=±2,y=±1所围成的两个顶点.
,A、B是四条直线x=±2,y=±1所围成的两个顶点.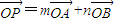 ,求证:动点Q(m,n)在定圆上运动,并求出定圆的方程;
,求证:动点Q(m,n)在定圆上运动,并求出定圆的方程;