题目内容
下列四个命题中,正确的是( )A.“m>n”是“
 ”的充分不必要条件
”的充分不必要条件B.命题“若a>b,则2a>2b-1”的否命题为“若a≤b,则2a≤2b-1”
C.已知p:存在实数x,使得
 :对任意实数x,都有x2-x+1>0,则命题“p∧¬q”是真命题
:对任意实数x,都有x2-x+1>0,则命题“p∧¬q”是真命题D.“对任意实数x,都有x2+1≥1”的否定是“存在实数x,使得x2+1≤1”
【答案】分析:若m>n,利用对应的指数函数为减函数可得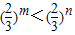 ;命题的否命题,条件与结论同时否定;p假q真,则命题“p∧¬q”是假命题;“对任意实数x,都有x2+1≥1”的否定是“存在实数x,使得x2+1<1”,从而可得结论.
;命题的否命题,条件与结论同时否定;p假q真,则命题“p∧¬q”是假命题;“对任意实数x,都有x2+1≥1”的否定是“存在实数x,使得x2+1<1”,从而可得结论.
解答:解:若m>n,则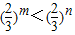 ,故A错误;
,故A错误;
命题的否命题,条件与结论同时否定,故B正确;
p假q真,则命题“p∧¬q”是假命题,故C错误;
“对任意实数x,都有x2+1≥1”的否定是“存在实数x,使得x2+1<1”,故D错误.
故选B.
点评:本题以命题为载体,考查指数函数的单调性,考查命题的否定与否命题,考查复合命题的真假判断,知识点多,需要一一判断.
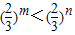 ;命题的否命题,条件与结论同时否定;p假q真,则命题“p∧¬q”是假命题;“对任意实数x,都有x2+1≥1”的否定是“存在实数x,使得x2+1<1”,从而可得结论.
;命题的否命题,条件与结论同时否定;p假q真,则命题“p∧¬q”是假命题;“对任意实数x,都有x2+1≥1”的否定是“存在实数x,使得x2+1<1”,从而可得结论.解答:解:若m>n,则
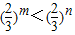 ,故A错误;
,故A错误;命题的否命题,条件与结论同时否定,故B正确;
p假q真,则命题“p∧¬q”是假命题,故C错误;
“对任意实数x,都有x2+1≥1”的否定是“存在实数x,使得x2+1<1”,故D错误.
故选B.
点评:本题以命题为载体,考查指数函数的单调性,考查命题的否定与否命题,考查复合命题的真假判断,知识点多,需要一一判断.

练习册系列答案
相关题目