题目内容
已知椭圆C的一个焦点为F(0,1),过点F且垂直于长轴的直线被椭圆C截得的弦长为
;P,Q,M,N为椭圆C上的四个点.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若
∥
,
∥
且
•
=0,求四边形PMQN的面积的最大值和最小值.
| 2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)若
| PF |
| FQ |
| MF |
| FN |
| PF |
| FM |
分析:(1)根据一个焦点为F(0,1),设出椭圆方程,再利用过点F且垂直于长轴的直线被椭圆C截得的弦长为
,求出几何量,即可得到椭圆的方程;
(2)设出直线方程,代入椭圆方程,求出|PQ|,|MN|,表示出面积,利用基本不等式,即可得到结论.
| 2 |
(2)设出直线方程,代入椭圆方程,求出|PQ|,|MN|,表示出面积,利用基本不等式,即可得到结论.
解答:解:(Ⅰ)由题圆C的一个焦点为F(0,1)知c=1
故可设椭圆方程为
+
=1(a>b>0)
过焦点F(0,1)且与长轴垂直的直线方程为y=c,设此直线与椭圆交于A,B两点
则|AB|=
,又|AB|=
,所以
=
,又b2=a2-c2=a2-1,
联立求得b2=1,a2=2,故椭圆方程为x2+
=1
(Ⅱ)由
∥
,
∥
知,点P,Q,F共线,点M,N,F共线,
即直线PQ,MN经过椭圆焦点F.又
•
=0知,PQ⊥MN
(i)当PQ斜率为零或不存在时,S=
|PQ||MN|=
×2a×
=2b2=2
(ii)当直线PQ存在且不为零时,可设斜率为k,则由PQ⊥MN知,MN的斜率为-
所以:直线PQ方程为:y=kx+1.直线MN方程为:y=-
x+1
将直线PQ方程y=kx+1代入椭圆方程2x2+y2-2=0,消去y并化简整理可得(2+k2)x2+2kx-1=0,
设P,Q坐标为P(x1,y1),Q(x2,y2),则x1+x2=-
,x1x2=-
…①
从而|PQ|=
|x1-x2|=
,将①代入化简得|PQ|=
,
将|PQ|中k换成-
可得|MN|=
所以S=
|PQ||MN|=
=
=
令f(k)=
=2-
=2-
因为k2+
≥2,所以2(k2+
)+5≥9,故0<
≤
所以
≤2-
<2,当且仅当k2=
即k=±1时,S=
综上(i)(ii)可知
≤S≤2,即四边形PMQN的最大面积为2,最小面积为
.
故可设椭圆方程为
| y2 |
| a2 |
| x2 |
| b2 |
过焦点F(0,1)且与长轴垂直的直线方程为y=c,设此直线与椭圆交于A,B两点
则|AB|=
| 2b2 |
| a |
| 2 |
| 2b2 |
| a |
| 2 |
联立求得b2=1,a2=2,故椭圆方程为x2+
| y2 |
| 2 |
(Ⅱ)由
| PF |
| FQ |
| MF |
| FN |
即直线PQ,MN经过椭圆焦点F.又
| PF |
| FM |
(i)当PQ斜率为零或不存在时,S=
| 1 |
| 2 |
| 1 |
| 2 |
| 2b2 |
| a |
(ii)当直线PQ存在且不为零时,可设斜率为k,则由PQ⊥MN知,MN的斜率为-
| 1 |
| k |
所以:直线PQ方程为:y=kx+1.直线MN方程为:y=-
| 1 |
| k |
将直线PQ方程y=kx+1代入椭圆方程2x2+y2-2=0,消去y并化简整理可得(2+k2)x2+2kx-1=0,
设P,Q坐标为P(x1,y1),Q(x2,y2),则x1+x2=-
| 2k |
| 2+k2 |
| 1 |
| 2+k2 |
从而|PQ|=
| 1+k2 |
| 1+k2 |
| (x1+x2)2-4x1x2 |
2
| ||
| 2+k2 |
将|PQ|中k换成-
| 1 |
| k |
2
| ||
| 2k2+1 |
所以S=
| 1 |
| 2 |
| 4(k2+1)2 |
| (2k2+1)(k2+2) |
| 4k4+8k2+4 |
| 2k4+5k2+2 |
| 4k4+10k2+4-2k2 |
| 2k4+5k2+2 |
令f(k)=
| 4k4+10k2+4-2k2 |
| 2k4+5k2+2 |
| 2k2 |
| 2k4+5k2+2 |
| 2 | ||
2(k2+
|
因为k2+
| 1 |
| k2 |
| 1 |
| k2 |
| 2 | ||
2(k2+
|
| 2 |
| 9 |
所以
| 16 |
| 9 |
| 2 | ||
2(k2+
|
| 1 |
| k2 |
| 16 |
| 9 |
综上(i)(ii)可知
| 16 |
| 9 |
| 16 |
| 9 |
点评:本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查四边形面积的计算,考查基本不等式的运用,属于中档题.

练习册系列答案
相关题目
 ,称圆心在原点O、半径是
,称圆心在原点O、半径是 的圆为椭圆C的“准圆”.已知椭圆C的一个焦点为
的圆为椭圆C的“准圆”.已知椭圆C的一个焦点为 ,其短轴的一个端点到点
,其短轴的一个端点到点 的距离为
的距离为 .
. 是椭圆C的“准圆”与
是椭圆C的“准圆”与 轴正半轴的交点,
轴正半轴的交点, 是椭圆C上的两相异点,且
是椭圆C上的两相异点,且 轴,求
轴,求 的取值范围;
的取值范围; ,过点
,过点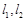 ,使得
,使得