题目内容
如图,已知椭圆C: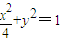 ,A、B是四条直线x=±2,y=±1所围成的两个顶点.
,A、B是四条直线x=±2,y=±1所围成的两个顶点.(1)设P是椭圆C上任意一点,若
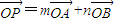 ,求证:动点Q(m,n)在定圆上运动,并求出定圆的方程;
,求证:动点Q(m,n)在定圆上运动,并求出定圆的方程;(2)若M、N是椭圆C上两个动点,且直线OM、ON的斜率之积等于直线OA、OB的斜率之积,试探求△OMN的面积是否为定值,说明理由.

【答案】分析:(1)设P的坐标,通过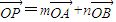 ,推出m,n与P的坐标的关系,推出定圆的方程.
,推出m,n与P的坐标的关系,推出定圆的方程.
(2)设M(x1,y1),N(x2,y2),利用直线OM、ON的斜率之积等于直线OA、OB的斜率之积,得到x1,x2的关系.求出MN的距离以及O到直线MN的距离,然后证明△OMN的面积是否为定值.
解答:解:(1)易求A(2,1),B(-2,1).…(2分)
设P(x,y),则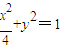 .由
.由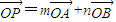 ,得
,得 ,
,
所以 ,即.故点Q(m,n)在定圆
,即.故点Q(m,n)在定圆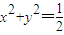 上.…(8分)
上.…(8分)
(2)设M(x1,y1),N(x2,y2),则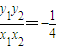 .
.
平方得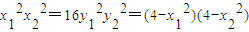 ,即
,即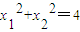 .…(10分)
.…(10分)
因为直线MN的方程为(x2-x1)y-(y2-y1)x+x1y2-x2y1=0,
所以O到直线MN的距离为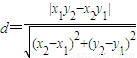 ,…(12分)
,…(12分)
所以△OMN的面积S= MN•l=
MN•l= |x1y2-x2y1|=
|x1y2-x2y1|=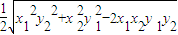
=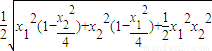 =
=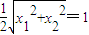 .
.
故△OMN的面积为定值1.…(16分)
点评:本题考查圆的方程的求法,点到直线的距离公式,弦长公式的应用,考查转化思想计算能力.
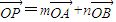 ,推出m,n与P的坐标的关系,推出定圆的方程.
,推出m,n与P的坐标的关系,推出定圆的方程.(2)设M(x1,y1),N(x2,y2),利用直线OM、ON的斜率之积等于直线OA、OB的斜率之积,得到x1,x2的关系.求出MN的距离以及O到直线MN的距离,然后证明△OMN的面积是否为定值.
解答:解:(1)易求A(2,1),B(-2,1).…(2分)
设P(x,y),则
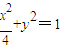 .由
.由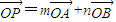 ,得
,得 ,
,所以
 ,即.故点Q(m,n)在定圆
,即.故点Q(m,n)在定圆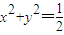 上.…(8分)
上.…(8分)(2)设M(x1,y1),N(x2,y2),则
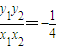 .
.平方得
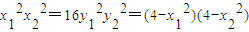 ,即
,即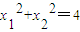 .…(10分)
.…(10分)因为直线MN的方程为(x2-x1)y-(y2-y1)x+x1y2-x2y1=0,
所以O到直线MN的距离为
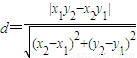 ,…(12分)
,…(12分)所以△OMN的面积S=
 MN•l=
MN•l= |x1y2-x2y1|=
|x1y2-x2y1|=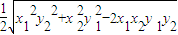
=
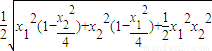 =
=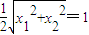 .
.故△OMN的面积为定值1.…(16分)
点评:本题考查圆的方程的求法,点到直线的距离公式,弦长公式的应用,考查转化思想计算能力.

练习册系列答案
相关题目
 如图,已知椭圆C:
如图,已知椭圆C: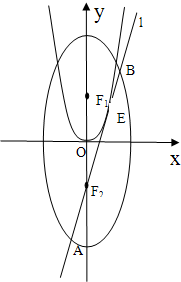 如图,已知椭圆
如图,已知椭圆 如图,已知椭圆C:
如图,已知椭圆C: 如图,已知椭圆
如图,已知椭圆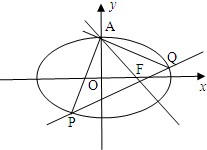 (2012•梅州一模)如图,已知椭圆C:
(2012•梅州一模)如图,已知椭圆C: