题目内容

【题目】已知全集U=R，集合A={x|1≤x＜5}，B={x|2＜x＜8}，C={x|﹣a＜x≤a+3}
（1）求A∪B，（UA）∩B；
（2）若C∩A=C，求a的取值范围．

【答案】
（1）解：由集合A={x|1≤x＜5}，B={x|2＜x＜8}，

所以A∪B={x|1≤x＜5}∪{x|2＜x＜8}={x|1≤x＜8}，

CUA={x|x＜1或x≥5}，∴（CUA）∩B={x|5≤x＜8}


（2）解：∵C∩A=C，∴CA

①当C=时，满足CA，此时﹣a≥a+3，得

②当C≠时，要使CA

则 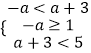，解得 ．

综上所述：a≤﹣1


【解析】（1）直接利用并集、补集和交集的概念求解；（2）由C∩A=C，∴CA，然后分C为空集和不是空集分类求解a的范围，最后取并集．

练习册系列答案
相关题目

【题目】设 ，其中 n 为正整数．
（1）求f(1),f(2),f(3) 的值；
（2）猜想满足不等式 f(n)<0 的正整数 n 的范围，并用数学归纳法证明你的猜想．

【题目】已知函数y=|log2x|的定义域为[ ，n]（m，n为正整数），值域为[0，2]，则满足条件的整数对（m，n）共有（ ）
A.1个
B.7个
C.8个
D.16个

【题目】已知复数z=lg（m2﹣2m﹣2）+（m2+3m+2）i，根据以下条件分别求实数m的值或范围．
（1）z是纯虚数；
（2）z对应的点在复平面的第二象限．

【题目】已知复数 ．
（1）若 z 为纯虚数，求实数 a 的值；
（2）若 z 在复平面上对应的点在直线 x+2y+1=0 上，求实数 a 的值．

【题目】已知 ．经计算得 ．
（1）由上面数据，试猜想出一个一般性结论；
（2）用数学归纳法证明你的猜想．

【题目】已知函数y=ln（2﹣x）[x﹣（3m+1）]的定义域为集合A，集合B={x| ＜0}
（1）当m=3时，求A∩B；
（2）求使BA的实数m的取值范围．

【题目】已知函数f（x）=lg（x+1），g（x）=2lg（2x+t）（t为参数）．
（1）写出函数f（x）的定义域和值域；
（2）当x∈[0，1]时，如果f（x）≤g（x），求参数t的取值范围．

【题目】（12分）如图，椭圆 （）的离心率，短轴的两个端点分别为B1、B2，焦点为F1、F2，四边形F1 B1F2 B2的内切圆半径为

（1）求椭圆C的方程；

（2）过左焦点F1的直线交椭圆于M、N两点，交直线于点P，设，，试证为定值，并求出此定值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网