题目内容
18．三棱锥各顶点的坐标分别为（0，0，0），（1，0，0），（0，2，0），（0，0，3），则三棱锥的体积为1．分析 由题意，C（0，0，0），A（1，0，0），B（0，2，0），P（0，0，3），则PC⊥平面ABC，CB⊥CA，利用两点间的距离可知AC，CB和PC，进而利用三棱锥体积公式求得答案．
解答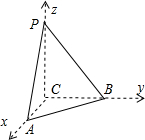 
解：由题意，C（0，0，0），A（1，0，0），B（0，2，0），P（0，0，3），则PC⊥平面ABC，CB⊥CA
则△ACB的面积=CA×CB÷2=1×2÷2=1，
则PC为三棱锥的高=3，
三棱锥的体积=△ACB的面积×高PC÷3=1×3÷3=1
故答案为：1．
点评 本题主要考查了点到面的距离计算和三棱锥的体积计算．点到平面的距离是立体几何的一个难点，其主要原因是垂线段难找，故垂线段是解题的关键．
练习册系列答案
黄冈天天练口算题卡系列答案
相关题目
10．若z1，z2∈R，则|z1•z2|=|z1|•|z2|，某学生由此得出结论：若z1，z2∈C，则|z1•z2|=|z1|•|z2|，该学生的推理是（ ）
| A． | 演绎推理 | B． | 逻辑推理 | C． | 归纳推理 | D． | 类比推理 |
6．某地区气象台统计，该地区下雨的概率是$\frac{4}{15}$，刮三级以上风的概率为$\frac{2}{15}$，既刮风又下雨的概率为$\frac{1}{10}$，则在下雨天里，刮风的概率为（ ）
| A． | $\frac{8}{225}$ | B． | $\frac{1}{2}$ | C． | $\frac{3}{8}$ | D． | $\frac{1}{10}$ |
13．已知等比数列{an}，若存在两项am，an使得aman=a32，则$\frac{1}{m}$+$\frac{4}{n}$的最小值为（ ）
| A． | $\frac{3}{2}$ | B． | $\frac{5}{3}$ | C． | $\frac{9}{4}$ | D． | $\frac{7}{6}$ |
10．已知△ABC利用斜二测画法画出的直观图是边长为2的正三角形，则△ABC的面积为（ ）
| A． | $\sqrt{3}$ | B． | 2$\sqrt{3}$ | C． | $\sqrt{6}$ | D． | 2$\sqrt{6}$ |
8．对于两个变量之间的相关系数r，下列说法中正确的是（ ）
| A． | |r|≤1且|r|越接近于1，相关程度越大；|r|越接近于0，相关程度越小 | |
| B． | |r|越小，相关程度越大 | |
| C． | |r|越大，相关程度越小；|r|越小，相关程度越大 | |
| D． | |r|越大，相关程度越大 |