题目内容
在整数集Z中,被5除所得余数为k的所有整数组成一个“类”,记为[k],
即[k]={5n+k丨n∈Z},k=0,1,2,3,4。 给出如下四个结论:
①2013∈[3];
②-3∈[2];
③Z=[0]∪[1]∪[2]∪[3]∪[4]
④“整数a,b属于同一“类”的充要条件是“a-b∈[0]”。
其中正确结论的个数是( )
| A.1 | B.2 | C.3 | D.4 |
D
解析试题分析:①依题意2013被5除的余数为3,则①正确;
②由于-3=-5+2,故-3∈[2],即②正确;
③整数集就是由被5除所得余数为0,1,2,3,4的整数构成,③正确;
④假设C中a=5n1+m1,b=5n2+m2,a-b=5(n1-n2)+m1-m2,a,b要是同类,
则m1-m2=0,所以a-b∈[0],
反之也成立,④正确;
故选D.
考点:命题的真假判断与应用;进行简单的合情推理.

练习册系列答案
相关题目
某个命题与正整数有关,若当 时该命题成立,那么可推得当
时该命题成立,那么可推得当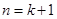 时该命题也成立,现已知当
时该命题也成立,现已知当 时该命题不成立,那么可推得( )
时该命题不成立,那么可推得( )
A.当 时,该命题不成立 时,该命题不成立 | B.当 时,该命题成立 时,该命题成立 |
C.当 时,该命题成立 时,该命题成立 | D.当 时,该命题不成立 时,该命题不成立 |
在 中,角
中,角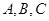 所对应的边分别为
所对应的边分别为 ,则
,则 是
是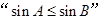 的( ).
的( ).
| A.充分必要条件 | B.充分非必要条件 |
| C.必要非充分条件 | D.非充分非必要条件 |
.“ ”是“
”是“ ”的( )
”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
命题“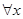 ∈R,
∈R,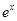 -x+1≥0”的否定是( )
-x+1≥0”的否定是( )
A.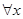 ∈R,lnx+x+1<0 ∈R,lnx+x+1<0 | B.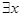 ∈R, ∈R,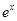 -x+1<0 -x+1<0 |
C.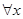 ∈R, ∈R,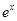 -x+1>0 -x+1>0 | D.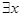 ∈R, ∈R,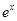 -x+1≥0 -x+1≥0 |
设 是等比数列,则“
是等比数列,则“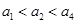 ”是“数列
”是“数列 是递增数列”的( ).
是递增数列”的( ).
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
若“0<x<1”是“(x-a)[x-(a+2)]≤0”的充分不必要条件,则实数a的取值范围是( )
| A.(-∞,0]∪[1,+∞) | B.(-1,0) |
| C.[-1,0] | D.(-∞,-1)∪(0,+∞) |
 的定义域为集合N,求:
的定义域为集合N,求:  ,
, 和
和 都是全集
都是全集 的子集,且有
的子集,且有 ,
, ,
, ,求集合
,求集合