题目内容
已知函数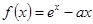 (
(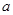 为常数)的图像与
为常数)的图像与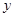 轴交于点
轴交于点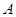 ,曲线
,曲线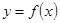 在点
在点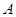 处的切线斜率为-1.
处的切线斜率为-1.
(1)求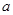 的值及函数
的值及函数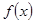 的极值;(2)证明:当
的极值;(2)证明:当 时,
时,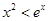 ;
;
(3)证明:对任意给定的正数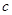 ,总存在
,总存在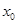 ,使得当
,使得当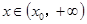 ,恒有
,恒有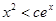 .
.
(1)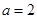 ,极小值为
,极小值为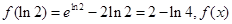 无极大值;(2)证明见解析;(3)证明见解析.
无极大值;(2)证明见解析;(3)证明见解析.
解析试题分析:
解题思路:(1)利用导数的几何意义求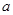 ,再进一步求极值;(2)构造函数
,再进一步求极值;(2)构造函数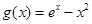 ,即证
,即证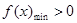 ;
;
(3)结合(2)的结论,对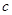 进行分类讨论.
进行分类讨论.
规律总结:这是一道典型的导函数问题,综合性较强,要求我们要有牢固的基础知识(包括函数的性质、常见解题方法、数形结合等).
试题解析:解法一:(1)由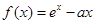 ,得
,得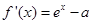 .又
.又 ,得
,得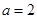 .所以
.所以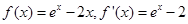 .令
.令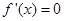 ,得
,得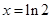 .当
.当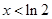 时,
时, 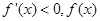 单调递减;当
单调递减;当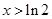 时,
时, 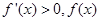 单调递增.所以当
单调递增.所以当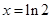 时,
时,  取得极小值,且极小值为
取得极小值,且极小值为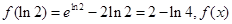 无极大值.
无极大值.
(2)令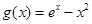 ,则
,则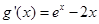 .由(1)得
.由(1)得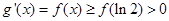 ,故
,故 在R上单调递增,又
在R上单调递增,又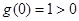 ,因此,当
,因此,当 时,
时, 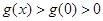 ,即
,即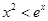 .
.
(3)①若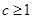 ,则
,则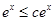 .又由(2)知,当
.又由(2)知,当 时,
时, 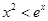 .所以当
.所以当 时,
时, 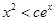 .取
.取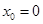 ,当
,当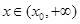 时,恒有
时,恒有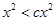 .
.
②若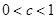 ,令
,令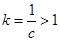 ,要使不等式
,要使不等式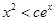 成立,只要
成立,只要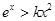 成立.而要使
成立.而要使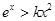 成立,则只要
成立,则只要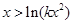 ,只要
,只要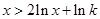 成立.令
成立.令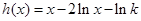 ,则
,则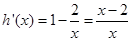 .所以当
.所以当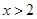 时,
时, 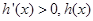 在
在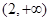 内单调递增.取
内单调递增.取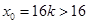 ,所以
,所以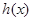 在
在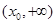 内单调递增.又
内单调递增.又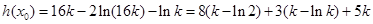 .易知
.易知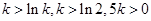 .所以
.所以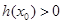 .即存在
.即存在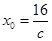 ,当
,当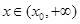 时,恒有
时,恒有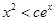 .
.
综上,对任意给定的正数c,总存在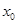 ,当
,当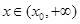 时,恒有
时,恒有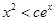 .
.
解法二:(1)同解法一
(2)同解法一
(3)对任意给定的正数c,取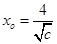
由(2)知,当x>0时,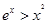 ,所以
,所以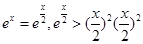
当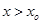 时,
时, 
因此,对任意给定的正数c,总存在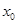 ,当
,当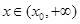 时,恒有
时,恒有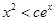 .
.
考点:1.导数的几何意义;2.导数在研究函数中的应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
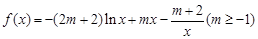 .
.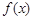 的单调性;
的单调性;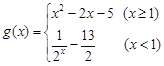 .当
.当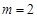 时,若对任意
时,若对任意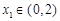 ,存在
,存在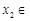
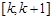 ,(
,(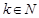 ),使
),使 ,求实数
,求实数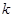 的最小值.
的最小值.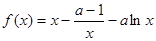
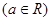 .
. 是函数
是函数 的极大值点,求
的极大值点,求 的取值范围;
的取值范围;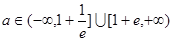 时,若在
时,若在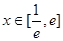 上至少存在一点
上至少存在一点 ,使
,使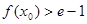 成立,求
成立,求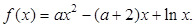
 时,求曲线
时,求曲线 在点
在点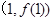 处的切线方程;
处的切线方程;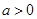 时,若
时,若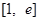 上的最小值为
上的最小值为 ,其中
,其中 是自然对数的底数,
是自然对数的底数, ,函数g(x)的导函数
,函数g(x)的导函数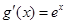 ,且
,且
 的极值;
的极值;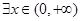 ,使得
,使得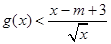 成立,试求实数m的取值范围:
成立,试求实数m的取值范围: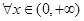 ,求证:
,求证: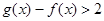
 的函数
的函数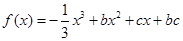 ,其导函数为
,其导函数为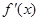 .记函数
.记函数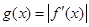 在区间
在区间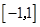 上的最大值为
上的最大值为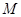 .
.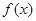 在
在 处有极值
处有极值 ,试确定
,试确定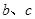 的值;
的值;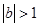 ,证明对任意的
,证明对任意的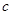 ,都有
,都有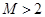 ;
;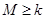 对任意的
对任意的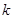 的最大值.
的最大值.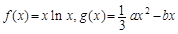 ,其中a,b∈R
,其中a,b∈R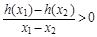 成立,试用a表示出b的取值范围;
成立,试用a表示出b的取值范围;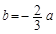 时,若
时,若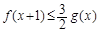 对x∈[0,+∞)恒成立,求a的最小值.
对x∈[0,+∞)恒成立,求a的最小值. .
. 在
在 处取得极值,求
处取得极值,求 内有极大值和极小值,求实数
内有极大值和极小值,求实数 的取值范围.
的取值范围. .
. 的极值(用含
的极值(用含 的式子表示);
的式子表示); 轴有3个不同交点,求
轴有3个不同交点,求