题目内容
已知函数 ,函数g(x)的导函数
,函数g(x)的导函数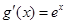 ,且
,且
(1)求 的极值;
的极值;
(2)若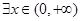 ,使得
,使得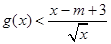 成立,试求实数m的取值范围:
成立,试求实数m的取值范围:
(3)当a=0时,对于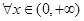 ,求证:
,求证: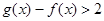
(1)当a≥0时, 没有极值;当a<0时,
没有极值;当a<0时, 取得极大值
取得极大值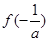 =
=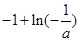 ;(2)
;(2)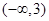 ;(3)见解析.
;(3)见解析.
解析试题分析:(1)求函数定义域、导数,按照a≥0,a<0两种情况讨论 的符号变化,由极值定义可求得
的符号变化,由极值定义可求得 的极值;(2)先由条件求出
的极值;(2)先由条件求出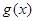 ,存在x∈(0,+∞),使得
,存在x∈(0,+∞),使得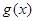 <
<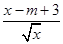 成立,即m<
成立,即m<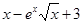 成立.令
成立.令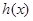 =
=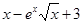 ,x∈(0,+∞),则问题等价于m<
,x∈(0,+∞),则问题等价于m<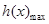 ,利用基本不等式可判定导数研究
,利用基本不等式可判定导数研究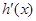 的正负时,从而判定出函数
的正负时,从而判定出函数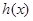 的单调性,从而可求得
的单调性,从而可求得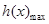 ;(3)当a=0时,先将
;(3)当a=0时,先将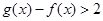 具体化为
具体化为 ,令
,令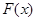 =
=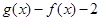 =
=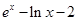 ,利用导数通过研究
,利用导数通过研究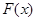 的单调性、极值,从而得出函数
的单调性、极值,从而得出函数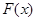 的图像性质,求出
的图像性质,求出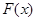 的最小值,只要证明最小值大于零即证明了
的最小值,只要证明最小值大于零即证明了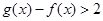 .
.
试题解析: (1)函数 的定义域为(0,+∞),
的定义域为(0,+∞), =
=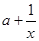 (
(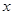 >0).
>0).
(i)当a≥0时, >0,
>0,
函数 在(0,+∞)上单调递增,故
在(0,+∞)上单调递增,故 没有极值;
没有极值;
(ii)当a<0时, =
=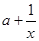 =
=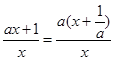 ,
,
当x∈(0,﹣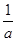 )时,
)时, >0;当x∈(﹣
>0;当x∈(﹣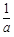 ,+∞)时,
,+∞)时, <0,
<0,
∴当x=﹣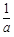 时,
时, 取得极大值
取得极大值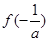 =
=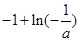 .
.
(2)∵函数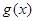 的导函数
的导函数 =
=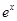 ,
,
∴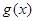 =
=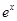 +c(其中c为常数)
+c(其中c为常数)
由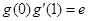 ,得(1+c)e=e,故c=0,
,得(1+c)e=e,故c=0,
∴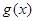 =
=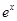 .
.
若存在x∈(0,+∞),使得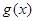 <
<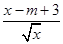 成立,即m<
成立,即m<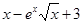 成立.
成立.
令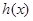 =
=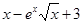 ,x∈(0,+∞),则问题等价于m<
,x∈(0,+∞),则问题等价于m<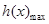 ,
,
∴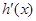 =1﹣
=1﹣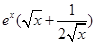 ,
,
∵当x∈(0,+∞)时,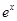 >1,
>1,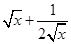 ≥
≥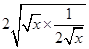 =
=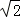 ,
,
∴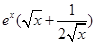 >1,故
>1,故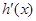 <0,
<0,
∴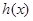 在(0,+∞)上单调递减,
在(0,+∞)上单调递减,
∴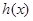 <
<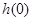 =3,故m<3.
=3,故m<3.
(3)解:当a=0时, =lnx,
=lnx,
令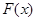 =
=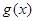 ﹣
﹣ ﹣2=
﹣2=
练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
 .
.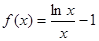 .
.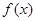 的单调性;
的单调性;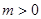 ,求
,求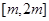 上的最大值;
上的最大值;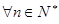 ,不等式
,不等式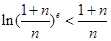 .
.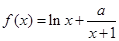 ,
, 为常数.
为常数. ,求函数
,求函数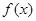 在
在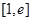 上的值域;(
上的值域;( 为自然对数的底数,
为自然对数的底数, )
) 在
在 上为单调减函数,求实数
上为单调减函数,求实数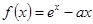 (
(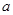 为常数)的图像与
为常数)的图像与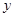 轴交于点
轴交于点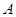 ,曲线
,曲线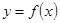 在点
在点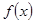 的极值;(2)证明:当
的极值;(2)证明:当 时,
时,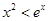 ;
;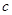 ,总存在
,总存在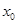 ,使得当
,使得当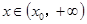 ,恒有
,恒有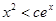 .
. .
.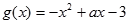 .
.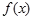 在区间
在区间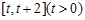 上的最小值;
上的最小值;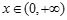 ,
,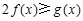 恒成立,求实数
恒成立,求实数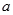 的取值范围;
的取值范围;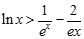 恒成立.
恒成立. ,对任意给定的正实数a,曲线y=F(x)上是否存在两点P,Q,使得△POQ是以O(O为坐标原点)为直角顶点的直角三角形,而且此三角形斜边中点在y轴上?请说明理由.
,对任意给定的正实数a,曲线y=F(x)上是否存在两点P,Q,使得△POQ是以O(O为坐标原点)为直角顶点的直角三角形,而且此三角形斜边中点在y轴上?请说明理由.
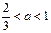 ,函数
,函数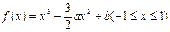 的最大值为1,最小值为
的最大值为1,最小值为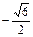 ,常数
,常数 的值是_____________.
的值是_____________.